Алгоритм распределения точек на плоскости

Question

[Алекс Смит]

Здравствуйте. Возникла такая задача реализовать распределение случайных точек на плоскости по разным правилам. В частности необходимо получить картинки похожие на эти:
1) С одним центром


2) С несколькими центрами


3) Более сложные варианты распределения: в виде спиралей, различных кривых, окружностей и т.д.

На данный момент у меня это все реализовано через достаточно тяжелый алгоритм распределения вероятностей по плоскости. Задается трехмерная функция, значение которой по оси Z является показателем уровня вероятности попадания точки в данную область плоскости. Благодаря этому алгоритму получается строить вот такие картинки

Однако данный алгоритм достаточно тяжел: приходится для каждой точки (а их могут быть сотни тысяч) вычислять значение трехмерной функции, оценивать уровень вероятности для данной координаты и т.д.

Я уверен, что есть более простые и эффективные способы решения данной задачи. Буду весьма благодарен за полезные ссылки по теме, общие идеи алгоритмов, а также за указание недочетов. Спасибо.

Comments

[Emin]

1. Нужны просто картинки, или массив точек потом как-то обрабатывается?
2. Картинку нужно получать именно формулой, или наложение фильтров, различных распределений друг на друга или регулирование прозрачности точек тоже допускается?

[Алекс Смит]

Нужно получить массив точек. Картинка лишь отображает их положение. Целью является именно заполнение двумерного массива.

Answer 1

[Emin]

Поскольку фигуры имеют центральную симметрию, то имеет смысл перейти к полярным координатам.
1. Сфера

for (var i:uint = 0; i < 10000; ++i)
{
       w = i;
       r = R * Math.random();

       // Преобразование в декартовые координаты
       // Задание цвета и размера точки
}

2. Наложение нескольких сфер с разными центрами (разные X0 и Y0 в декартовых координатах)
3. Для получения кольца можно использовать следующую подход

for (var i:uint = 0; i < 10000; ++i)
{
       w = i;
       r = R + dR * Math.random();

       // Преобразование в декартовые координаты
       // Задание цвета и размера точки
}

Дальше кольца с разными радиусами просто накладываются друг на друга.
4. Более хитрые фигуры получаются аналогичных образом:

r =  r(w) + dR * Math.random();

Например, спираль:

for (var i:uint = 0; i < 10000; ++i)
{
       w = 0.05 * i;
       r = 5 * w + dR * Math.random();

       // Преобразование в декартовые координаты
       // Задание цвета и размера точки
}

Коэффициенты подбираются в зависимости от конкретного случая.

Comments

[Алекс Смит]

Я пробовал использовать логарифмическую спираль, но основной проблемой для меня встало, как равномерно рассеять точки вдоль относительно этой самой спирали. Кривая спирали является осью, относительно которой точки рассеиваются и вот тут у меня уже ничего придумать не получилось.

[Emin]

А если воспользоваться вот такими формулами:

	w = Math.log(i)
	r = Math.exp(w) + dR * Math.random();

Т.е. брать для w не равномерный шаг, а логарифмический. Обратная функция для экспоненты обеспечит равномерный шаг для r.

[Алекс Смит]

Спасибо — попробую обязательно.

Answer 2

[Akson87]

Первое, что пришло в голову:
1) Делаем битмэп с единицами там, где мы хотим иметь центр скопления (можно также рисовать окружности, спирали итд итп)
2) Строим 2д карту вероятности появления точки путем нахождения минимального расстояния до ближайшей единицы на битмэпе для каждого пикселя
3) Для каждого пикселя изображения ставим ставим точку с вероятностью, полученной в пункте 2

Первый шаг — это ваш вход, второй шаг считается очень быстро, если делать это приближенно, третий шаг можно замечательно распараллелить.

Если хочется получить кластеры, можно применять алгоритм итеративно и случайным образом рассчитывать параметры «точки» радиус, скорость затухания, яркость, цвет итд итп.

Answer 3

[cyberXndr]

Для разных фигур будут соверщенно разные алгоритмы.
Пару дней назад тоже решал эту задачу.

общий алгоритм такой:
1)создаем двухмерный массив с нулями
2)выбираем произвольную точку — основу круга. Выбираем радиус.
3)выбираем формулу какой либо фигуры (в моем случае круг)
4)проходим по всем элементам массива, проверяя принадлежность текущей точки к фигуре. Если точка принадлежит фигуре — ставим в данное поле массива единичку с случайным шансом.
5)увеличиваем радиус
6)повторяем 1-5 пару раз.

думаю выходит не совсем удачно в плане производительности, но работает.
подробную реализацию (для круга) скину в лс по запросу.

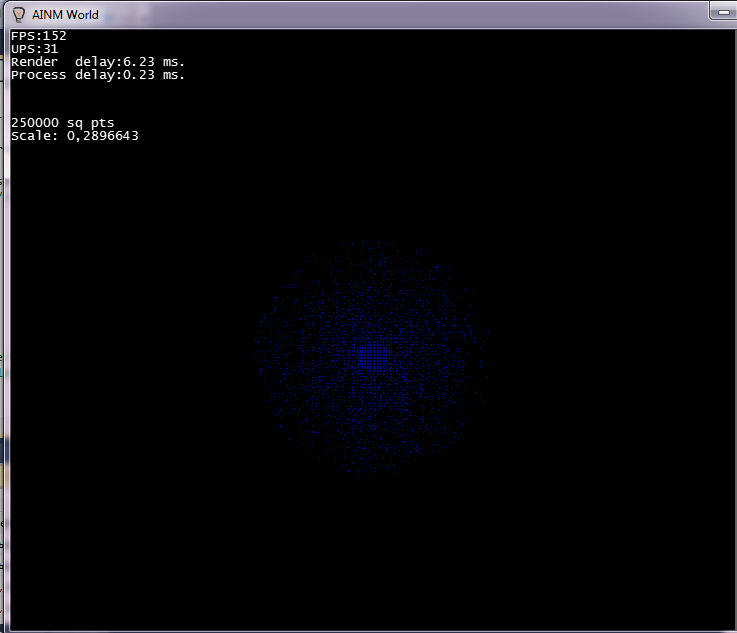
На выходе получается вот что: (очень зависит от коэффициентов, за пару минут можно подобрать нужную плотность)



Над чем работаете, если не секрет?

Comments

[Алекс Смит]

Игра :)

[Алекс Смит]

Круги заметны, согласен. Но простое линейное уменьшение вероятности даст конфигурацию вероятности в виде конуса и будет тоже не совсем то что нужно. Я на самом деле достаточно долго бился, пытаясь подобрать функцию дающую красивое распределение, как у настоящих скоплений. И это получилась функция: z = K / ln (C + sqrt(x*x + y*y)), где K и С коэфициенты, манипулируя которыми можно регулировать высоту и крутизну графика.

Answer 4

[anmipo]

Вот здесь расписаны три подходящих метода.
В частности, можно взять метод усечения, расширив его на одну размерность:
1) выбираем случайную точку на плоскости (то есть берём два случайных числа x и y от генератора с равномерным распределением);
2) генерируем ещё одно число z в пределах 0..1;
3) если z > f(x, y), где f — ваша 3D-функция распределения плотности вероятности — рисуем точку в (x, y);
4) goto 1 (пока не надоест).

Этот метод позволяет управлять «насыщенностью» картины, постепенно уточняя её. Приемлемый результат получится быстрее, чем при переборе всех точек.

Comments

[Алекс Смит]

Сейчас именно так и реализовано. Проблема в том, что функция, которая имеет такую конфигурацию в пространстве достаточно тяжела для расчета и генерирование картинки из 50000 точек занимает достаточно много времени (примерно 10 минут на моем ноутбуке).

[Алекс Смит]

Ссылка хорошая, спасибо

Answer 5

[lam0x86]

Вот ещё вариант: Преобразование Бокса — Мюллера