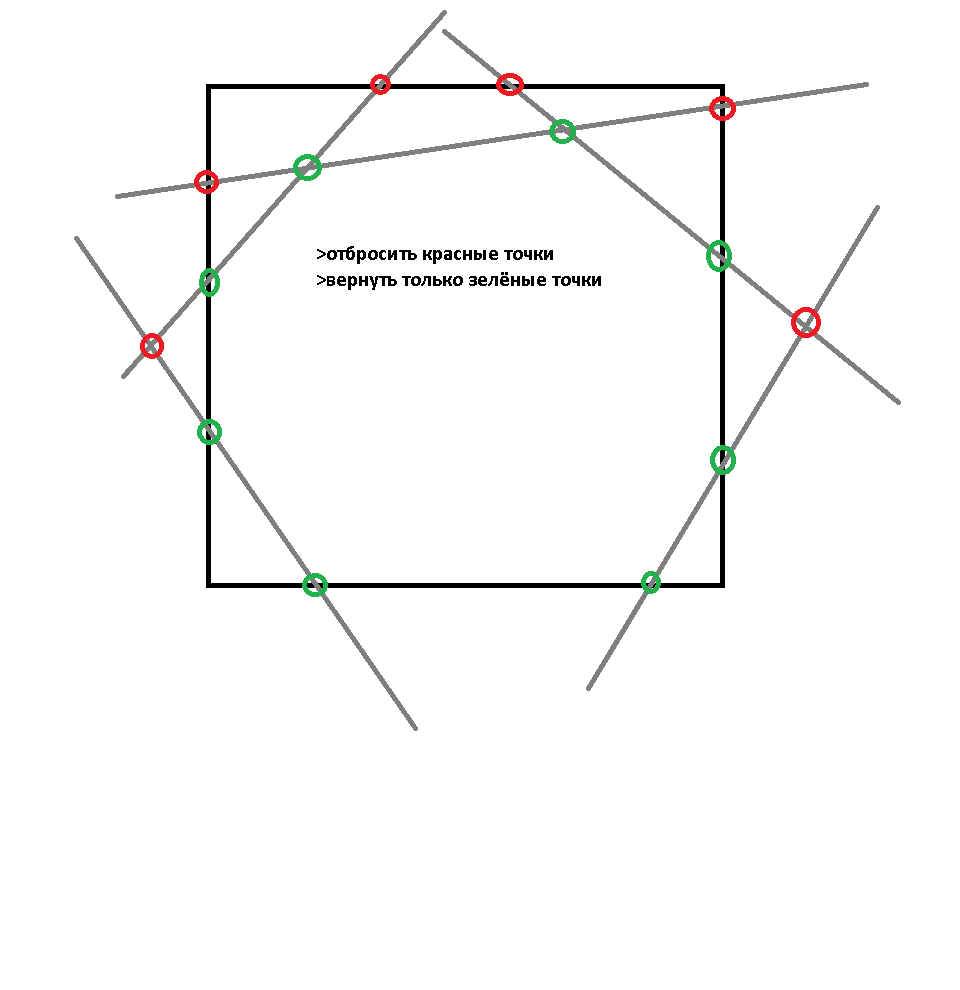
Для начала, надо бы уточнить условие. Ибо непясно, по какому принципу выбирается, какая из двух отсекаемых прямой половин берется в ответ.
Картинке удовлетворяет такая интерпретация: Берется область, остекаемая прямыми, содержащая центр квадрата. Предполагаем, что прямые через центр не проходят.
Тогда каждая прямая задает полуплоскость допустимых точек, да и сам квадрат можно задать 4-мя такими полуплосокстями и вам надо найти пересечение всех их.
Эта задача решается за O(n log n). Задайте каждую прямую в виде ax+by+c=0. Т.ч. вектор {a,b} выпущенный с прямой, торчит в сторону полуплоскости, которую надо взять. Если вдруг не так, то надо поменять знак у всех трех коэффициентов.
Разбейте все прямые на 2 множества, те - которые смотрят "вверх" и те, которые смотрят "вниз". Если вектор нормали имеет положительную y координату - это смотрит вверх. Вертикальные прямые можно включить, допустим, в верхнее множество.
В каждом множестве построим ломанную, отделяющую нужную область. Это будет выпуклая область с двумя бесконечными лучами в конце.
Потом отсортируйте все прямые по углу наклона вектора {a,b}. Это можно сделать без тригонометрии, сравнивая векторы по векторному произведению. Ну, или просто какую-нибудь функцию вроде atan2() используйте.
Потом будем поддерживать ломанную, описывающую пересечение первых k проуплоскостей. Изначально это просто одна прямая (для первой полуплоскости). Будем хранить это как стек из прямых и рядом стек из точек пересечения. Изначально там только одна прямая и 0 точек пересечения.
Потом добавляем полуплоскости по одной. Пока последняя вершина на ломанной не лежит в нужной полуплоскости, выбрасываем ее. Для этого убираем из обоих стеков последний элемент. Это можно проверить, просто подставив координаты точки в уравнение ax+by+c. Если даст отрицательное значение - выбрасываем.
Если точек не осталось, или точка лежит где надо, то новую прямую надо пересечь с последней прямой. Точку пересечения и новую прямую добавляем в стек.
В конце мы получили две ломанные, огибающие нужное пространство сверху и снизу. Надо их пересечь.
Для этого выкинием сверхней ломанной все крайние точки, которые отсекаются последней и первой прямой в нижней ломанной. И наоборот. В конце, пересечения двух бесконечных лучей слева и справа добавляем в ответ.