Какую кривую эффективнее построить на множестве [0; 1] — Безье, нецелочисленную степенную или гиперболу?

Question

[Eugene Y]

Добрый день!

Ищу наиболее эффективный алгоритм приближенного вычисления параметризируемой кривой на множестве [0; 1], отмеченной на рисунке оранжевым цветом:

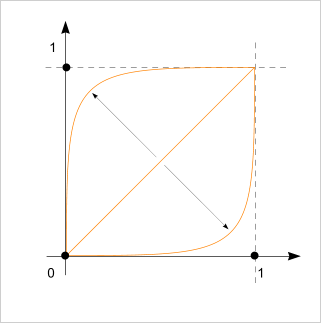
Важна возможность менять кривизну, получая очень большую и очень маленькую производную на концах, или просто иметь линейное приращение.
На ум приходят
- возведение в степень с показателем, меняющимся примерно в границах [0,1 ; 10]
- кривая Безье
- масштабированная и смещенная гипербола
Возможно, существуют и альтернативные варианты, но я их не нашел.
Какой из алгоритмов вычисления этих кривых эффективнее?
Кривая вычисляется раз в секунду, в каждой кривой примерно 50 000 точек.

Answer 1

[Koss1024]

Здесь как родная ложится Рациональная кривая Безье второго порядка

Базис
b0(t) = (1-t)^2
b1(t) = 2*(1-t)
b2(t) = t^2

Точки
P0 = (0, 0)
P1 = (1, 0) (или 0,1)
P2 = (1, 1)

Тогда обычная кривая имеет вид: B(t) = sum_by_i(b(i) *P(i))

Рациональная B(t) = sum_by_i(b(i) * P(i) * w(i) ) / sum_by_i(b(i, w(i))

Где w(i) это веса вершин установив значение w(1) > 1 вы получите свой результат

На пальцах кривая стремится приблизиться к вершине с весом > 1 и наоборот

Answer 2

[Сергей]

x(t) = t * log(a*t)
y(t) = t * log(b*t)

t изменяется [0;1].

В зависимости от a и b получаете нужный вид кривой. В частном случае a=b.

Comments

[Сергей]

Впрочем, конечно формулы должны быть немного другими. Но основная мысль вам понятна ? :)

[Eugene Y]

Честно говоря, нет :)

[EndUser]

Смысл в том, что через две точки можно провести практически любые кривые. Форма кривой зависит от функции. В данном случае Бегемот предлагает вам выбрать функцию по вкусу самостоятельно, но обязательно в виде "нормализованного" по t уравнения.

Answer 3

[Андрей]

Субъективно гипербола выглядит наиболее эффективно, тем более что позиция изменения второй координаты вычисляется аналитически, что позволяет прорисовывать "хвостики" весьма быстро.
Насколько серьезно Вы готовы озадачиться ускорением ?

Comments

[Eugene Y]

Если это не требует прочтения толстых книг и прохождения курсов, то готов :) Эта вещь мне нужна для желаемой, но не критичной функциональности. То есть желание есть, но не фанатичное.

Answer 4

[Mrrl]

Если надо, чтобы кривую можно было провести через любую точку квадрата, то гипербола, пожалуй, лучше. Уравнение выглядит привлекательно: (a^2-1)*x*y+(x-a^2*y)=0, найти значение a для любой точки, через которую проходит кривая, несложно. Немного сложнее её нарисовать, чтобы точки были расположены с нужной густотой.
Я думал над чем-нибудь вроде y^a+(1-x)^a=1, но оно вряд ли подойдёт, хоть и симметрично: семейства кривых при a<1 и a>1 получаются не симметричными друг другу.

Comments

[Eugene Y]

Кривую надо провести через две фиксированные точки: (0,0) и (1,1).

[Mrrl]

Это понятно. И оба уравнения, которые я написал, это учитывают. Но вопрос в том, как определяется оставшаяся степень свободы - ещё одной точкой, через которую должна пройти кривая, или как-нибудь иначе (слайдером регулировки параметра?)

[Eugene Y]

Любым образом, главное - гладкость кривой и эффективность. На данный момент рисуется кривая степенной функции и слайдер на GUI меняет значение показателя степени.