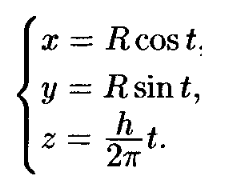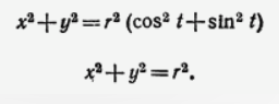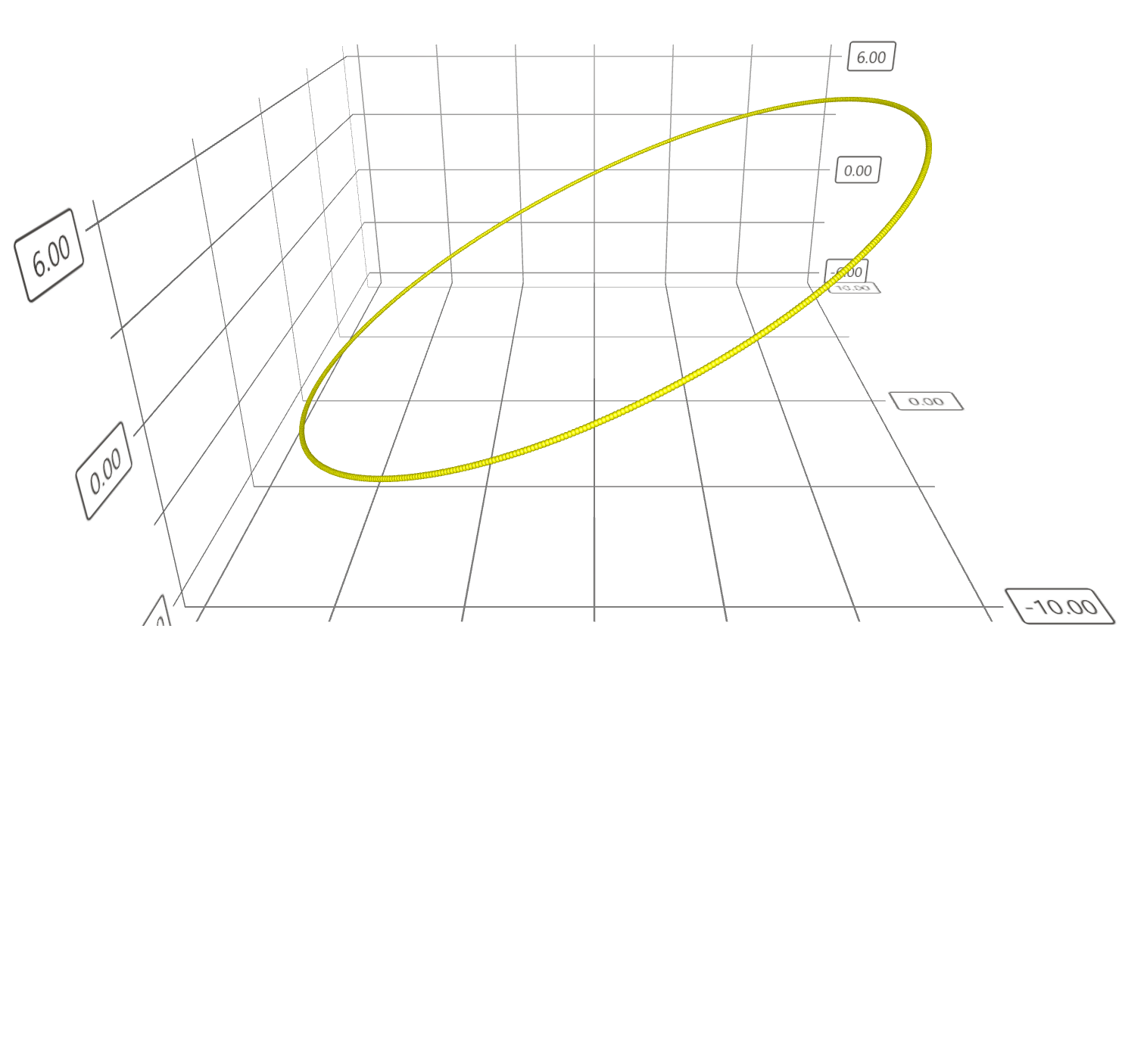
xx = r * Math.cos(t);
yy = r * Math.sin(t);
zz = 6 * Math.cos(t);
Каждая кривая должна иметь возможность возвращать трехмерную точку и первую производную (трехмерный
вектор) для каждого параметра t вдоль кривой.
x = -1 * r * sin(t)
y = r * cos(t)
z = cos(t)
x=A*sin t
y=B*cos t
z=C*t