. A B C
A - 4 1
B 4 - 1
C 1 1 -int n = Integer.parseInt(reader.readLine());
for (int i = 1; i <= n/3; i++) {
for (int j = i; j <= (n-i)/2; j++) {
System.out.println("Числа " + i + " + " + j + " + " + (n-i-j));
}
}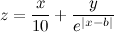
#include <iostream>
#include <vector>
#include <set>
#include <time>
std::set<std::string> subSeqs;
struct _element {
char digit;
int count;
};
std::vector<_element> elemSeq;
void recurse(std::vector<_element>::iterator elemRest, std::string subSeqHead) {
bool fin = (elemRest+1 == elemSeq.end());
for (int i = 0; i <= elemRest->count; i++, subSeqHead += elemRest->digit)
if (fin)
subSeqs.insert(subSeqHead);
else
recurse(elemRest+1, subSeqHead);
}
void main(void)
{
int i;
_element element;
std::string initialSeq = "1234567890123";
std::cout << "Initial sequence: " << initialSeq << "\n";
clock_t start = clock();
element.digit = initialSeq[0];
element.count = 1;
for (i = 1; i < initialSeq.length(); i++) {
if (element.digit == initialSeq[i])
element.count++;
else {
elemSeq.push_back(element);
element.digit = initialSeq[i];
element.count = 1;
}
}
elemSeq.push_back(element);
recurse(elemSeq.begin(), "");
clock_t finish = clock();
i = 0;
std::cout << "Elements: (";
for (std::vector<_element>::iterator t = elemSeq.begin();
t != elemSeq.end(); t++) {
if (i++ != 0)
std::cout << ", ";
std::cout << "{'" << t->digit << "', " << t->count << "}";
}
std::cout << ")\n";
std::cout << subSeqs.size()-1 << " unique subsequences\n";
std::cout << "Calculation time " << finish-start << " clicks, ";
std::cout << ((float)(finish-start))/CLOCKS_PER_SEC << " sec\n";
/* for (std::set<std::string>::iterator t = subSeqs.begin();
t != subSeqs.end(); t++) {
std::cout << *t << "\n";
} */
}Initial sequence: 8246
Elements: ({'8', 1}, {'2', 1}, {'4', 1}, {'6', 1})
15 unique subsequences
Calculation time 0 clicks, 0 sec
================================================================
Initial sequence: 88885
Elements: ({'8', 4}, {'5', 1})
9 unique subsequences
Calculation time 0 clicks, 0 sec
================================================================
Initial sequence: 12345678901234567890
Elements: ({'1', 1}, {'2', 1}, {'3', 1}, {'4', 1}, {'5', 1}, {'6', 1}, {'7', 1},
{'8', 1}, {'9', 1}, {'0', 1}, {'1', 1}, {'2', 1}, {'3', 1}, {'4', 1}, {'5', 1},
{'6', 1}, {'7', 1}, {'8', 1}, {'9', 1}, {'0', 1})
1043455 unique subsequences
Calculation time 4383 clicks, 4.383 sec
================================================================
Initial sequence: 11223344556677889900
Elements: ({'1', 2}, {'2', 2}, {'3', 2}, {'4', 2}, {'5', 2}, {'6', 2}, {'7', 2},
{'8', 2}, {'9', 2}, {'0', 2})
59048 unique subsequences
Calculation time 187 clicks, 0.187 secфункция рекурсия(набор, результат) {
если набор пуст {
если результат уникален {
добавить результат в список уникальных
}
}
((цифра, количество), следующий_набор) = набор;
для i от 0 до количество {
рекурсия(следующий_набор, результат+(цифра i раз));
}
}
рекурсия(исходный_набор, '');
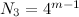
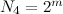
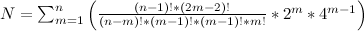
+----+---------------------+---------------------+
| n | без унарных минусов | с унарными минусами |
+----+---------------------+---------------------+
| 1 | 1 | 2 |
| 2 | 5 | 18 |
| 3 | 41 | 290 |
| 4 | 320 | 5'938 |
| 5 | 5'073 | 136'770 |
| 6 | 64'469 | 3'379'794 |
| 7 | 859'385 | 87'547'746 |
| 8 | 11'853'949 | 2'345'800'050 |
| 9 | 167'763'361 | 64'477'920'386 |
| 10 | 2'422'342'053 | 1'807'930'569'874 |
+----+---------------------+---------------------+2 3
0 0
1 1
1 2print ("%d %d" %(x2, y2)) Исходный массив
0 8 0 0 10
8 0 4 0 0
0 4 0 6 16
0 0 6 0 2
10 0 16 2 0
-- Шаг 1 -----
0 8 0 0 10
8 0 4 0 18
0 4 0 6 16
0 0 6 0 2
10 18 16 2 0
-- Шаг 2 -----
0 8 12 0 10
8 0 4 0 18
12 4 0 6 16
0 0 6 0 2
10 18 16 2 0
-- Шаг 3 -----
0 8 12 18 10
8 0 4 10 18
12 4 0 6 16
18 10 6 0 2
10 18 16 2 0
-- Шаг 4 -----
0 8 12 18 10
8 0 4 10 12
12 4 0 6 8
18 10 6 0 2
10 12 8 2 0
-- Шаг 5 -----
0 8 12 12 10
8 0 4 10 12
12 4 0 6 8
12 10 6 0 2
10 12 8 2 0// Инициализируем C, надо заменить на ввод исходных данных
$C = array(1, 1, 1, 0, 0, 1, 1, 1, 0, 1);
$N = count($C);
// Добавляем в начало и конец нули
array_unshift($C, 0);
$C[] = 0;
// Создаём массив P, заполняем 0 и N+1 элементы нулями
$P[0] = 0;
$P[$N+1] = 0;
// Заполняем чётные ячейки
for ($i = 1; $i <= $N; $i += 2)
$P[$i+1] = $P[$i-1] ^ $C[$i];
// Заполняем нечётные ячейки
if (($N&1) == 0) {
// Вариант с чётным количеством ячеек
for ($i = $N; $i >= 1; $i -= 2)
$P[$i-1] = $P[$i+1] ^ $C[$i];
} else {
// Вариант с нечётным количеством ячеек
$P[1] = 0;
for ($i = 1; $i <= $N; $i -= 2)
$P[$i-1] = $P[$i+1] ^ $C[$i];
}
// Выводим результат
for ($i = 1; $i <= $N; $i++)
print $P[$i];