




В такой (уточненной) постановке задаче интересная и нетривиальная.
Позвольте предложить некоторое огрубление, которое по моему мнению исходя из предметной области не сильно отдалит субоптимальное решение от оптимального, но позволит уйти от геометрии к дискретной математике :
Введем в указанном помещении декартовы координаты так, чтобы препятствия находились строго по границам единичных клеток.
Добавим следующие предположения/ограничения:
а) источники сигнала размещаем только в центрах клеток,
б) считаем, в каждом из четырех диагональных направлений сигнал не виден в клетках, размещенных за углом (углами) любого препятствия (см. рис.)
в) в четырех прямых направлениях сигнал очевидно не виден за первым же препятствием а также нигде далее этой координаты (см.рис.).
Как результат для каждой ячейки как потенциального места расположения сигнала возможно определить булеву матрицу доступности ячеек.
В целом задача сводится к тому, чтобы найти минимальный набор таких выбранных матриц (соответствующих ячейкам расположения источников), который бы обеспечивал полное покрытие помещения.
Мне кажется, что при больших размерах матриц эффективно это реализуемо только алгоритмами эвристического поиска (я сторонник генетических алгоритмов, но конечно есть и другие подходы). 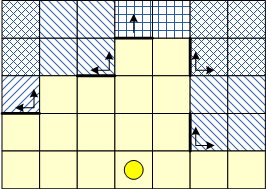

У любой расстановки есть какая-либо цель. Какая у Вас ?
Покрыть всё пространство сигналом ?
Или наоборот не допустить пересечения сигналов в точке ?
Равны ли диаметры окружностей ?
По какому критерию оптимизируем ?
Задача пока что неясна.

При дифференцированном платеже ежемесячный платеж нефиксирован, X - величина переменная, поэтому Вы и не можете найти формулу. Либо Вы некорректно сформулировали то, что Вам хочется вычислить.


