Почему в d-ичном куче ребёнок выисляется по такой формуле?

Question

[Александр]

Имеем кучу с количеством потомков на один узел равным d. Пронумеруем в нём все элементы с 1 до n, где n - кол-во всех узлов. нумеровать узлы будем по очереди в каждом уровне, чтобы получилось примерно так:


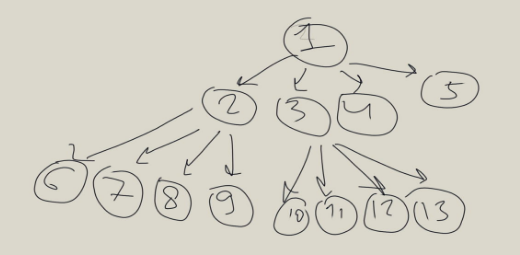
Я узнал, что формула расчёта всех детей в таком дереве такая:
{(i−1)d+2,…,min{n,(i−1)d+d+1}}
Кто-нибудь может объяснить или хотя бы натолкнуть в верном направлении почему эта формула работает? Как она сформировалась? (тут min для случая когда вышли за предел дерева)

Answer 1

[Wataru]

Удобнее, если нумеровать вершины с 0. Тогда дети будут d*i+1...d*i+d. Ваша формула получается из этой простым перенумерованием (вычитанием и добавлением единицы в нужные места). Далее я буду рассуждать об этой формуле.

В этой формуле очевидно, что отцом у вершины k (с номером > 0) будет floor((k-1)/d). Далее, видно, что для двух разных вершин номера их детей не будут пересекаться никак (потому что это отрезки из d номеров, сдвинутые как минимум на d относительно друг друга). Так же можно доказать по индукции, что все числа от 1 до бесконечности будут соответсвовать какой-то вершине в дереве (мы же можем получить отца по формуле (x-1)/d, по индукции он уже в дереве, а значит и текущий номер соответствует вершине).

Интитивно же, умножение на d появляется потому, что на каждом следующем уровне вершин ровно в d раз больше чем на предыдущем. Все дети одной вершины идут подряд, значит будут в формуле +1,+2... для детей.

Comments

[Александр]

Наводка с вершиной с 0 оказалась очень полезной, спасибо