Почему в решениях с одинаковой сложностью существенная разница во времени расчета?

Question

[DennyD314]

Всем привет!
Недавно встретилась довольно простая задача: дан массив целых чисел и число "a", нужно найти первое ближайшее к "a" число в массиве.
Сразу пришел на ум не самый оптимальный вариант - посчитать для всех чисел в массиве модуль разности с a, найти минимальный и за третий проход остановиться при совпадении.
Потом понял, что решить задачу можно еще как минимум 3 способами (через key в min, через reduce, через простой самописный алгоритм) и решил измерить время расчета для каждого способа.

def time_deco(func):
    @wraps(func)
    def wrapper(*args, **kwargs):
        start = datetime.now()
        res = func(*args, **kwargs)
        return (datetime.now() - start).total_seconds()
    return wrapper

 

@time_deco
def with_min(a, l):
    return min(l, key=lambda x: abs(a-x))

 

@time_deco
def with_reduce(a, l):
    return reduce(lambda x, y: x if abs(a-y) >= abs(a - x) else y, l)

 

@time_deco
def with_map(a, l):
    z = min(map(lambda x: abs(a-x), l))
    for i in l:
        if abs(a-i) == z:
            return i

 

@time_deco
def traditional_way(a, l):
    value = l[0]
    i = abs(a - value)
    for item in l:
        if abs(a - item) < i:
            i = abs(a - item)
            value = item
    return value
 

my_funcs = [with_min, with_reduce, with_map, traditional_way]

 

a = random.randint(0, 500000000)

 
random_list_100 = [random.randint(0, 100) for _ in xrange(100)]
random_list_100k = [random.randint(0, 100000) for _ in xrange(100000)]
random_list_1kk = [random.randint(0, 1000000) for _ in xrange(1000000)]
random_list_100kk = [random.randint(0, 100000000) for _ in xrange(100000000)]
random_list_200kk = [random.randint(0, 200000000) for _ in xrange(200000000)]
random_list_300kk = [random.randint(0, 300000000) for _ in xrange(300000000)]

 
for_df = dict()


for func in my_funcs:
    for_df[func.__name__] = [func(a, random_list_100),
                             func(a, random_list_100k),
                             func(a, random_list_1kk),
                             func(a, random_list_100kk),
                             func(a, random_list_200kk),
                             func(a, random_list_300kk),
                            ]

 
df = pd.DataFrame(data=for_df)

Результаты оказались довольно странными для меня:


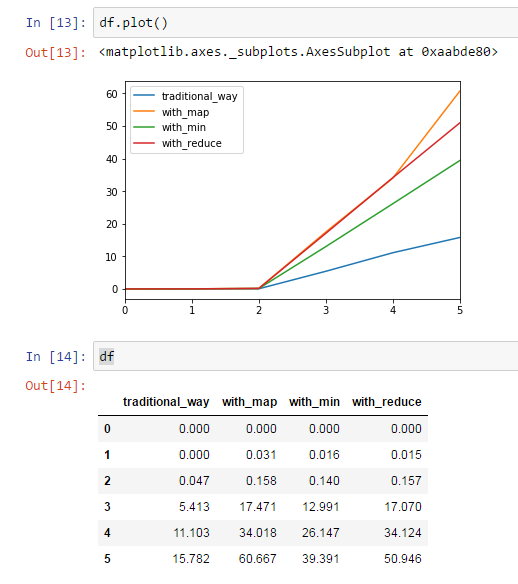
Я не могу понять, почему min и reduce считаются в разы дольше чем самописный вариант, ведь нахождение нужного элемента во всех случаях производится за 1 проход, а min, на сколько я понимаю, работает так же как я расписывал в traditional_way.

Comments

[res2001]

Добавьте еще реализацию аналогичную with_min, но с использованием numpy массивов, numpy.min() и numpy.abs(). Было бы интересно посмотреть на результат.

[Даша Циклаури]

сколько аллокаций в памяти производится для каждого варианта?

[DennyD314]

Даша Циклаури, думаю, примерно одинаково

[Даша Циклаури]

DennyD314, лучше конкретно в цифрах, как ответили ранее могут быть накладные расходы reduce например дорогая операция

Answer 1

[res2001]

Виноваты накладные расходы.
В traditional_way они минимальны.
Замените лямбды вычислением промежуточного массива содержащего abs(a-x) в остальных случаях и получите дополнительный прирост производительности.

Comments

[DennyD314]

Странная ситуация, встретив такую задачу на практике, я , зная что min принимает key, захочу воспользоваться именно ей, так как это красивое краткое решение, встроенная функция, а оказывается оно уступит в скорости простому самописному алгоритму в 4 раза ?

[res2001]

DennyD314, Зная, что вы передаете в функцию лямбду, вы должны сразу подумать, что эта лямбда будет вызываться и это дополнительные накладные расходы. А когда у вас в массиве 100500 элементов и на каждый нужно вызвать лямбду, то это уже будет заметно.

[res2001]

DennyD314, Кроме того я согласен с ответом dmshar - это то же имеет место быть.
Когда нужно обрабатывать большое количество данных, то надо использовать numpy его массивы и его функции для работы с массивами, а не родные питоновские структуры.
Я практически уверен, что реализация with_min с использованием numpy array станет лидером по производительности (без лямд, конечно).

[DennyD314]

res2001, давай попробуем, скинь функцию с np, которая, ты считаешь опередит все остальные, я запущу на массивах до 200кк.

[res2001]

Что-то типа этого:

import numpy as np
def with_min_np(a, l):
    return np.min(np.abs(l-a))

random_list_np_100 = np.random.randint(0, 100, size=100)
with_min_np(a, random_list_np_100)

[DennyD314]

res2001,

Функция такая:

@time_deco
def with_np(a, l):
    array = np.asarray(l)
    return array[np.abs(array - a).argmin()]

Проверял несколько раз, тенденция похожая, при 200кк элементов считается быстрее traditional_way.
Оставлю на ночь с 300, 400, 500кк, посмотрим, подтвердится ли.

[res2001]

DennyD314, думаю, что значительное время отъедает asarray. Лучше бы его из функции убрать - ты же не замеряешь создание массива в других функциях.

[DennyD314]

res2001, я поэтому на нижней строчке скрина и привел время его исполнения. Но не уверен, что убирать его будет корректно, все таки, по умолчанию, мы работаем со стандартными типами данных, то есть это тоже относится к функции - преобразование в np.array

[res2001]

DennyD314, Когда начинаешь работать с подобными (большими) массивами данных стандартные структуры уже не катят и нужно полностью переходить на numpy/scipy. Поэтому убрать asarray из функции будет вполне корректно.
Функции numpy поддерживают преобразования "по месту", т.е. будут изменять входной массив (или им можно передавать уже заранее сформированный массив). Это еще больше может ускорить их работу - не нужно будет выделять и инициализировать память под возвращаемый массив.

PS: у интела есть своя сборка питона с оптимизированными версиями некоторых библиотек, в т.ч. numpy/scipy, обещают ускорение в 20 раз по сравнению со стандартными версиями. Оптимизировали с помощью Intel MKL.

[DennyD314]

И по поводу накладных расходов хотел уточнить, не знаешь способ, как отразить это наглядно, почему 3 варианта с лямбдами выполняются медленнее.

[DennyD314]

res2001, Я имею в виду, что это будет не совсем корректно в рамках поставленной задачи, так как по условию подразумевается, что входные данные - список и число.

[res2001]

DennyD314, Сделай аналогичные варианты без лямбд - на одном графике разницу сразу будет видно.

[res2001]

DennyD314,

список и число

Опять же можно сделать 2 варианта, чтоб показать, что еще есть куда расти, если немного скорректировать задание.

Answer 2

[jcmvbkbc]

Почему в решениях с одинаковой сложностью существенная разница во времени расчета?

Я отвечу на вопрос из заголовка: потому что сложность алгоритма говорит о том, как он будет вести себя при неограниченном увеличении размерностей входных данных. И больше ни о чём. Т.е. нельзя имея два линейных алгоритма сказать, что они будут работать одинаковое время. Но можно имея линейный и квадратичный алгоритм сказать, что начиная с какого-то момента линейный всегда будет работать быстрее.

Comments

[dmshar]

В данном случае - все три алгоритма линейны. Только один имеет временнУю сложность O(N), второй 2*О(N), третий 3*O(N). И первый при любых N будет работать (почти) в три раза быстрее третьего. Просто на малых N это сложно обнаружить. Обратите внимание на шкалу Х, которая на самом деле нелинейна ( а черте-какая) - между 0 и 1 разница в 1000 раз, между 1 и 2 - в 10 раз, между 2 и 3 - в 100 раз, между 3 и 4 - в 2 раза, между 4 и 5 - в 1.5 раза).

[DennyD314]

да, в глобальном смысле это понятно, но хотелось бы понять так же, почему расчет при использовании встроенной функции min, которую я бы и использовал при всех подобных задачах, выполняется дольше в несколько раз ?

Answer 3

[dmshar]

"Я вам не скажу за всю Одессу" :-), но давайте сравним только with_map(a, l) и traditional_way(a, l). В обоих функциях присутствует цикл (for item in l:) который выполняется примерно за одинаковое время. Но with_map содержит еще и строку
z = min(map(lambda x: abs(a-x), l)) , которая сначала выполняет map(lambda x: abs(a-x), l) -
еще один проход по массиву, а в полученном результате ищет min - т.е. пробегает по списку еще раз. Итого - три прохода по массиву, вместо одного в traditional_way. С остальными функциями - примерно та-же история. (Например min(l, key=lambda x: abs(a-x)) - это как минимум два прохода по вашему списку).

Comments

[DennyD314]

Насчет with_map - это понятно.
Насчет min - не уверен, что min реализована таким образом, что вычисление производится за несколько проходов.

[dmshar]

DennyD314,
сам min() вычисляется за один проход. Но у вас параметры min создаются в динамике. Т.е. один проход - подготовка списка, второй проход - поиск минимума в списке.

[DennyD314]

Мне так не кажется, реализации найти не смог, но мне думается, что при наличии key lamdba функция применяется к элементу, а потом идет сравнение просто и происходит это за 1 проход.