Как определить, попадает ли точка в заштрихованную область?

Question

[dsfsaegf]

С кругом и эллипсом более-менее разобрался, но с линией вообще не могу понять, что делать.

Answer 1

[Cheypnow]

Записываешь функцию, по которой строятся линии, между которыми надо проверить лежит ли точка.
Подставляешь X точки в функцию, вычисляешь Y для этой функции.
Сравниваешь с Y точки. Если они равны, точка лежит на линии, если нет, лежит выше или ниже соответственно.
И просто выставляешь необходимые условия проверки, как должна лежать точка, выше или ниже заданных линий.

Answer 2

[Griboks]

А при чём тут C#? Это обычная математическая задачка. Если X<0, то Y должна лежать под прямой, иначе над прямой.
Можете использовать какую-нибудь библиотеку, можете пофантазировать с Rectangle.Contains.

Comments

[dsfsaegf]

Например при том, что нужно решить на нем?

[Griboks]

dsfsaegf, вы не можете записать формулу на C#? Я могу помочь с этим. Пишите формулу.

Answer 3

[Sumor]

Круг:
(x - x0)^2+(y-y0)^2 < R^2 - множество точек внутри круга
(x - x0)^2+(y-y0)^2 > R^2 - множество точек вне круга
R - радиус круга, x0, y0 - координаты центра

Эллипс:
((x - x0)/a)^2+((y-y0)/b)^2 < 1 - множество точек внутри эллипса
((x - x0)/a)^2+((y-y0)/b)^2 > 1 - множество точек вне эллипса
a, b - радиусы эллипса

Прямые:
x < 0 - множество точек левее оси 0Y
x > 0 - множество точек правее оси 0Y
y < 0 - множество точек ниже оси 0X
y > 0 - множество точек выше оси 0X
ax+by < c множество точек ниже прямой, заданной уравнением ax+by = с
ax+by > c множество точек выше прямой, заданной уравнением ax+by = с

Для вашей задачи:
1. Находите нужные коэффициенты для всех прямых и кривых.
2. Выясняете для каждого уравнения знак, который получается при попадании точки в заштрихованной области
3. Создаёте набор тестов для точки.

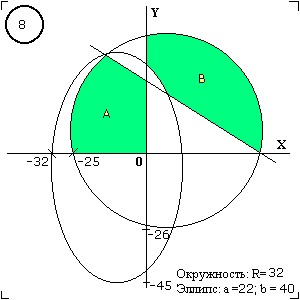
Например для зоны B:
Точка должна быть внутри круга, вне эллипса и выше прямой, то есть должны выполняться следующие неравенства (коэффициенты a, b x0, y0 для каждого неравенства свои):
(x - x0)^2+(y-y0)^2 < R^2
((x - x0)/a)^2+((y-y0)/b)^2 > 1
ax+by > c
Дальше для тестовой точки проверяете неравенства, и если они все правильные - точка принадлежит заштрихованной области.