Математика движения — как связать положение объектов через формулы кривой безье?

Question

[kisel]

Всем привет.

Прошу помочь с математикой движения. Никак не соображу где найти и как применить правильные формулы.

Мне нужно связать положение объекта вдоль оси Y с положением скролла, но зависимость не линейная. И мне необходимо иметь возможность эту зависимость настраивать. Поэтому я хочу как-то связать положение объекта и скролла через формулы кривых безье.

Я нашел формулы кривых безье , но никак не соображу как их применить в моем случае. Там разложена векторная форма на формулы для каждой проекции, но мне так не подходит. Мне бы подошло если бы я мог из известной проекции на ось Y получить t, а уже с помощью t получить X. Но мне не хватает знаний для инверсии формулы.

Вот график зависимости


Подтолкните пожалуйста в правильном направлении. Спасибо.

Comments

[d'Ivan]

кривая на иллюстрации по виду напоминает сигмоиду.

Answer 1

[AngReload]

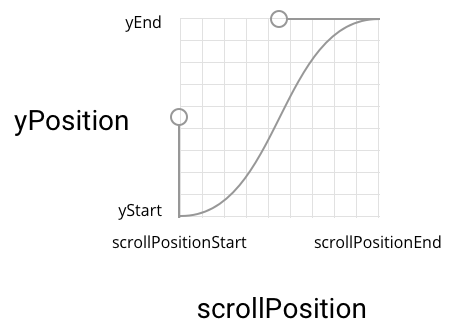
Судя по тому, что при некоторых значениях точек кривая может пересекаться сама с собой, простого решения нет.

На СО в подобном вопросе для точек

P0 = (X0,Y0)
P1 = (X1,Y1)
P2 = (X2,Y2)
P3 = (X3,Y3)

предлагают численно решать уравнения:

X(t) = (1-t)^3 * X0 + 3*(1-t)^2 * t * X1 + 3*(1-t) * t^2 * X2 + t^3 * X3
Y(t) = (1-t)^3 * Y0 + 3*(1-t)^2 * t * Y1 + 3*(1-t) * t^2 * Y2 + t^3 * Y3

при t от 0 до 1.

Я думаю, вам лучше задавать зависимость каким-то более надёжным способом. Кубическим сплайном, например.

UPD: маленькая библиотека находящая Y по X - https://github.com/gre/bezier-easing

Comments

[Николай Чуприк]

Вот-вот, зачем кривые Безье. Можно что попроще взять, особенно, если это для визуальных эффектов. Для начала стоит определиться и затем ограничить класс кривых.

Answer 2

[Вячеслав Рычков]

В Вашем тексте есть ссылка на запись "формулы кривых Безье", где описан Алгоритм де Кастельжо. Его запрограммировать проще на мой взгляд, пусть это будет метод PointF LinP(Point[ ] p, double t), который для координат 4-х точек, заданных в массиве p для любого t на отрезке [0,1] вычисляет координаты точки q (q.X, q.Y).
Реализация алгоритма, см в c-sharp.pro/?p=1164 .
Далее важно, чтобы Ваша кривая Безье была однозначной функцией (по смыслу задачи для движка). Тогда для заданного положения движка yz на отрезке [Start, End] методом деления отрезка [0,1] пополам найдете такое t, для которого | yz - q.Y | < eps. Тогда искомое X = q.X.

Answer 3

[profesor08]

Если прям охота посмотреть как это выглядит в коде то вот https://github.com/gre/bezier-easing, там все исходники.

Если хочешь прям вот взять и применять готовое, то аналогично ссылка выше, либо gsap и ease-visualizer

Answer 4

[Karpion]

Нарисованный Вами график нормально описывается функцией типа синуса в интервале от -Pi/2 до +Pi/2, только надо подогнать координаты.

Ну или можно взять функцию типа x-x^3 в интервале от -1/sqrt(2) до +1/sqrt(2). Координаты тоже надо будет подогнать.

Тейлор как бы намекает, что оба предложенных мной варианта похожи вовсе не случайно.