Как выделить наиболее связные группы элементов в графе?

Question

[Андрей Рогов]

Есть множество эллементов. Пары элементов могут быть связаны. Как выделить связные группы, и разделить их в местах, где связей мало?

Например

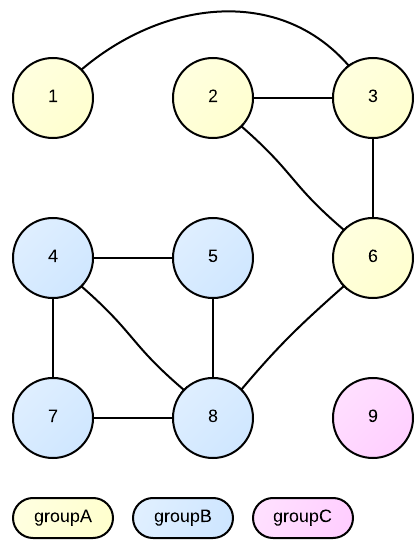
Не сложно выделить связную группу из элементов (1,2,3,4,5,6,7,8). Человеческим взглядом не сложно определить, что в этой группе есть тонкое место — единственная связь между элементами 6 и 8.
Как алгоритмически искать такие тонкие места и делить группы?
Вот исходная матрица из примера:
_ 0 1 0 0 0 0 0 0
0 _ 1 0 0 1 0 0 0
1 1 _ 0 0 1 0 0 0
0 0 0 _ 1 0 1 1 0
0 0 0 1 _ 0 0 1 0
0 1 1 0 0 _ 0 1 0
0 0 0 1 0 0 _ 1 0
0 0 0 1 1 1 1 _ 0
0 0 0 0 0 0 0 0 _
Буду рад любым материалам на русском языке или на языках программирования.

Добавлю, что из groupA не нужно удалять элемент 1, т.к. связь может и тонкая, но на этой связи к группе привязан только один элемент и данная связь вполне его выдержит. Тонкое место может состоять и из нескольких связей, если они соединяют подгруппы с большим колличеством элементов. И еще желательно рассмотреть ситуацию, с взвешенными связами:


P.S. Дискретную математику и т.д. давно не использовал, мог перепутать терминалогию.

Answer 1

[demolishka]

Почти то, что вам нужно, называется поиск мостов — ребер, удаление которых делает граф(в частности компоненту связности) несвязным.
Почитать об этом можно тут.

Answer 2

[totally_nameless]

То, что вы описываете очень напоминает задачу “graph partitioning”. en.wikipedia.org/wiki/Graph_partition
Если есть желание разобраться – посмотрите работы Gerorge Karypis. Он живой классик в этой области и его пакет Metis является state-of-art на сегодня. Если у вас ну очень большой граф, то можно использовать параллельную версию ParMETIS. Еще существует пакет Zoltan разработанный в рамках проекта Trilinos в Sandia National Lab. Примечателен тем, что использует гиперграф подход, что дает лучшее (в теории) качество разбиения. Однако у них явные проблемы с производительностью, да и сборка Trilinos – то еще удовлольствие. Вообще, для более детального анализа нужно знать, что у вас за граф: характерные размеры и степень связности (т.е. заполненость матрицы связности).
Удачи...
P.S. русскоязычной терминологией владею слабо, так что заранее прошу прощения за англицизмы...

Answer 3

[SeptiM]

Может быть нужен поиск минимального сбалансированного разреза? Как вариант можно сформулировать так: разбить вершины графа на две доли равного размера, чтобы число ребер между ними было минимально.

Здесь есть кое-что: theory.stanford.edu/~trevisan/cs359g/

Answer 4

[Seter17]

Может это поможет?

А если граф взевешнный — то наверно подойдет использование задачи о потоке

Answer 5

[alexkselk]

Это не кластерный ли анализ? (см. ту же википедию)