т.е. голова должна быть направлена в направлении движения
Направление движения будет вектор = касательная к кривой в данной точке * (вектор скорости/ значение скорости)
mathserfer.com/theory/kiselev2/node64.html
Вот тут есть как ее найти.
Производная в точке программно вычисляется через определение производной отношение разницы значений, см. определение частной производной через предел и как через нее найти полную производную.
Я понимаю, что через произвольные точки необходимо строить кривые, но никак не могу сообразить как определять корректно случайные точки, чтобы можно было построить нормальную кривую. Плюс как быть с виражами?
Чтобы траектория была гладкая - надо генерировать больше точек. Чтобы были дуги - использовать тригонометрические функции.
Главное правило, которое поможет:
* нужна цикличность - cos/sin etc
* нужно сглаживание между некоторым границами - sigmoid
* нужен рост - функции высшего порядка
В данном случае - нужна 2d функция, которая будет принимать x, y и возвращать z, подобная картина будет ее проекцией на 2d-плоскость
Берешь функцию:
f(x(t1), y(t1)) = a*cos(x(t1))^k + b * sin(y(t1))^t + O, где a,b,k,t, O - переменные, которые рандомно подбираешь для придания уникального вида, t1 - время, f(x(t1),y(t1)) - высота мухи по z, в зависимости от ее координат по x,y
Я хз как привести практический пример, поэтому приведу в python, некая гипотетическая пьяная муха или обдолбанный раптором комар

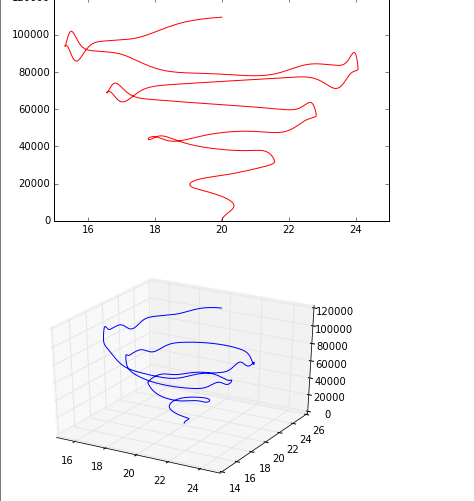
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def func(x, y, a, b, t, k, O):
return a * np.power(np.sin(x), t) + b * np.power(np.cos(y), k) + O
t = 5
k = 5
theta = np.linspace(-4 * np.pi, 4 * np.pi, 1000)
time = np.linspace(0, 5, num=1000)
a = 10
b = 10
x = time * np.sin(theta) + a
y = time * np.cos(theta) + b
z = np.asarray([func(x[i], y[i], a, b * i, t, k, 100) for i in range(len(x))])
plt.plot(x, z, 'r')
plt.show()
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(x, y, z)
Короче вектор в каком направлении двигаться ясен. Тупо перебирай функции генерации x, y и z пока не найдешь нужную красотульку