Как найти угол поворота объекта (компьютерная графика)?

Question

[Plant]

Задача:
Даны две картинки img1 и img2, на которых изображён исследуемый объект.
Объект на img1 повернули на произвольный угол вокруг произвольной точки принадлежащей этому объекту.
Результатом является изображение img2.
Границы объектов (до и после) мы можем вычислить и они будут заданы набором точек (x, y).

Вопрос:
Возможно ли найти точку, вокруг который был произведён поворот и угол поворота?
Точка поворота всегда принадлежит объекту на изображении img1.
Переноса и масштабирования нет, только поворот.
Внутри исследуемого объекта информация минимальна, поэтому возможно исследовать только границы.

Пример:
Img1 - до


Img2 -после


Результат

Answer 1

[Mrrl]

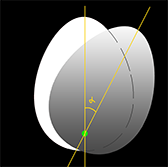
1) строите границы Г1, Г2.
2) для каждой считаете:
- центр масс (x0,y0)
- три интеграла: a11=int((x-x0)^2), a12=a21=int((x-x0)*(y-y0)), a22=int((y-y0)^2)
- собственные значения m1,m2 (m1 < m2) и собственные вектора v1,v2 матрицы ((a11 a12) (a21 a22)).
Пусть это было вычислено для Г1, а для Г2 получается m1', m2', v1', v2'.
Если искажений при повороте нет, то m1=m1', m2=m2'. Угол поворота определяется углом z между v1 и v1' (но надо сообразить, в какую сторону). К сожалению, он определён с точностью до 180 гр - так что надо будет как-нибудь сравнить варианты поворота на z и на z+180, и выбрать лучший. Допустим, что это z.
Осталось найти точку, при повороте вокруг которой на угол z точка (x0,y0) переходит в (x0',y0'). Проще всего записать это в комплексных числах: p0=x0+i*y0, p1=x0'+i*y0', f=exp(i*z). Если искомый центр c, то f*(p0-c)=p1-c, откуда c=(p1-f*p0)/(1-f).
И всё. Ничего сложного, первый курс ангема...

Answer 2

[Дмитрий Ковальский]

Если вы можете найти координаты пары точек на указанных осях - можете попробовать вычислить через скалярное произведение векторов.