Ребята, начал решать задачи по проекту Эйлера. Решил уже примерно 75 штук, но осталось несколько задачек, которые мне не совсем даются на пути окончания первой сотни задач. Я неплохо знаю математику, анализ, но совсем не учил ни комбинаторику, ни теорию вероятности, ни, тем более, что-то связанное с подобным поиском. Тут решения два : использовать динамическое программирование, либо комбинаторику. Брут тут реален, но это займет ну очень много времени.
Своим умом допер, что :
При N=20(кол-во исходов в одну сторону):
x = 2N! / (N! * N!)
x = 2*20! / (20! * 20!)
x = 137846528820(ответ верный)
Но, опять же, я не совсем понимаю механику работы поиска : количество исходов для любой клетки - максимум 40 вариантов(20 вниз и 20 вправо), но каким образом тут нам помогает факториал? И как это можно решить другим способом? Какие формулы нужно использовать, а также какую область математики, чтобы находить подобные решения без танцев с бубном?
P.S. решал на Python
Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
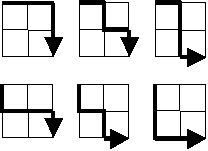
How many such routes are there through a 20×20 grid?
P.S.S. Вариант в переводе -
euler.jakumo.org/problems/view/15.html
Спасибо!
