Друзья, передо мной стоит задача нарисовать сплайн Безье, состоящий из набора квадратичных кривых Безье (второго порядка, параболы) при помощи одной из технологий/платформ, работающих с GPU. Собственно профильная платформа это Adobe Flash Stage3D, но речь в вопросе идет об алгоритме, поэтому это не так важно. Важен лишь факт отсутствия каких-либо готовых решений в виде расширений/библиотек, которые, насколько я понимаю, имеют место быть, например, в OpenGl.
Одним из важных моментов является тот факт, что мне хотелось бы отказаться от триангуляции сегмента кривой и создания сложной геометрии из множества треугольников для одного конкретного сегмента, а обойтись одним (возможно несколькими) треугольником на сегмент. Причиной почему, надеюсь, это может быть возможно, является фиксированная толщина сегмента кривой - 1-2px, при длине кривой в десятки раз ее превышающей.
В настоящее время я использую алгоритм, описанный в работе Loop/Blinn
research.microsoft.com/pubs/78197/p1000-loop.pdf или GPUGems3
http.developer.nvidia.com/GPUGems3/gpugems3_ch25.html
Сейчас фрагментный шейдер выглядит так:
float4 QuadraticPS(float2 p : TEXCOORD0,
float4 color : COLOR0) : COLOR
{
// Gradients
float2 px = ddx(p);
float2 py = ddy(p);
// Chain rule
float fx = (2*p.x)*px.x - px.y;
float fy = (2*p.x)*py.x - py.y;
// Signed distance
float sd = (p.x*p.x - p.y)/sqrt(fx*fx + fy*fy);
// Linear alpha
float alpha = thickness - abs(sd);
if (alpha > 1) // Inside
color.a = 1;
else if (alpha < 0) // Outside
clip(-1);
else
// Near boundary
color.a = alpha;
return color;
}
что позволяет получать на выходе подобное изображение:

Как мы видим - было бы прекрасно, если бы мы могли получить сегмент кривой Безье в одном треугольнике - но на участках, близлежащих к углам, толщина линии меняется (поскольку часть ее как бы переходит в отрицательную область). Что при отображении реального сплайна приводит к следующему эффекту:
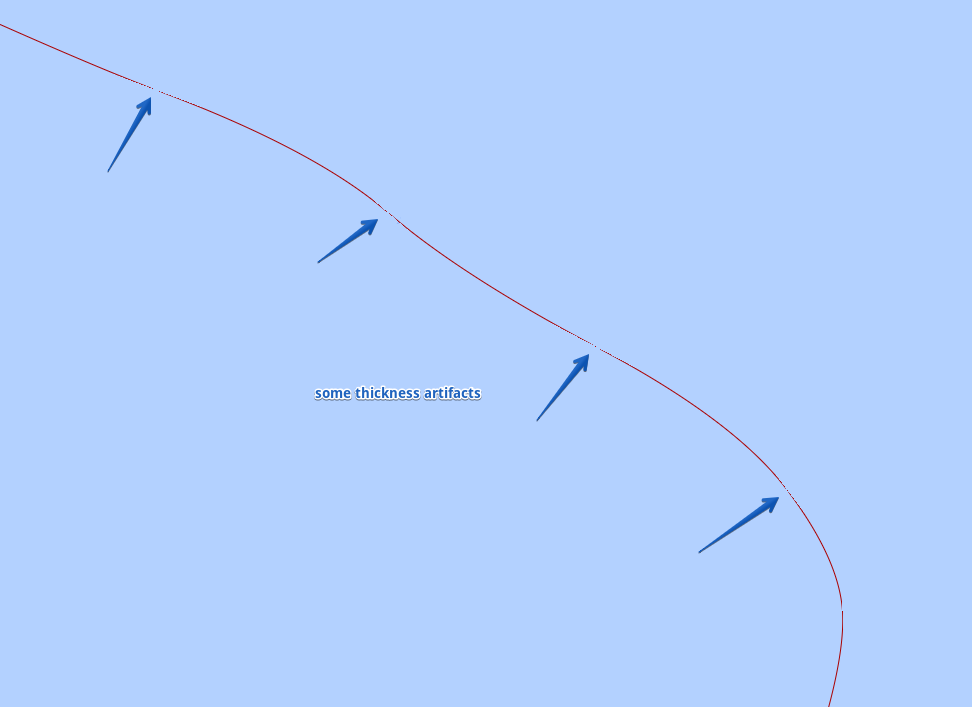
Подскажите пожалуйста каким образом можно решить данную проблему и можно ли действительно обойтись лишь несколькими треугольниками (для отображения "отрицательных" участков кривой рядом с углами)?
Любая помощь - на вес золота!

