Код на Python для расчёта "в лоб" (перебором) и выявления закономерностей:
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
from itertools import product
def process(existing, required):
for opcount in xrange(existing+required):
for combo in product('dcv', repeat=opcount):
buffer = 0
smiles = existing
data_y = [existing]
for char in combo:
if char == 'd':
smiles -= 1
elif char == 'v':
smiles += buffer
else:
buffer = smiles
data_y.append(smiles)
if smiles == required:
data_x = xrange(opcount+1)
plt.plot(data_x, data_y, linewidth=1)
print required, data_y
return ''.join(combo)
return '-'
for required in xrange(2, 101):
plt.clf()
plt.grid(True)
plt.title('Target: %s' % required)
plt.autoscale(enable=True, axis='both', tight=False)
for existing in xrange(1, (required//2)+1):
result = process(existing, required)
plt.savefig('{:02d}.png'.format(required), dpi=96, bbox_inches='tight')
Задача распадается на 2:
1) Если M >= N div 2, то нужно удалить всё до половины, скопипастить, и по необходимости удалить 1 смайл.
2) Если п.1 не выполняется, то нужно рассчитать делители N (если N простое - то взять следующие несколько чисел больше N) и спуститься к ближайшему наибольшему делителю N, который меньше M. Удалять смайлы, чтобы попадать в наблюдаемые на картинках горизонтальные уровни, соответствующие делителям.
В общем случае решение не единственное - например, соседние группы D и V можно смешивать в любых последовательностях: DDVVV = VVVDD = VDVDV = ...
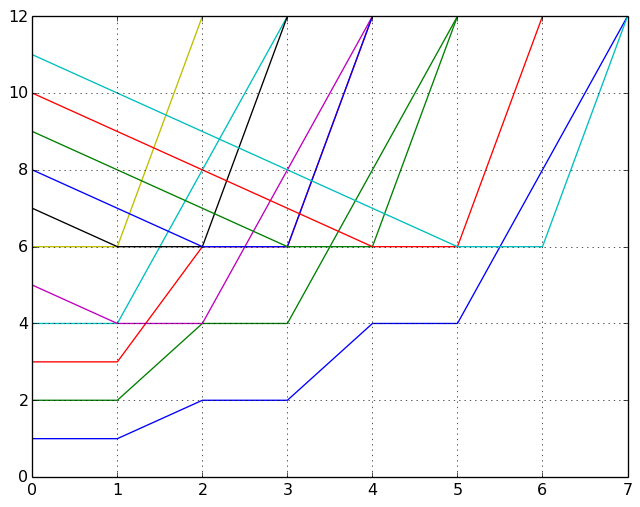
N=12. Для M=5 видим DCVV (фиолетовая линия). Уровни (делители) - 6, 4, 3, 2, 1:
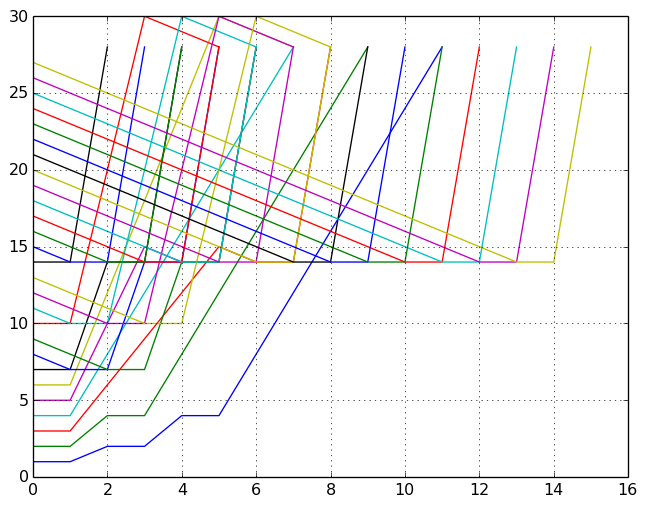
N=28:
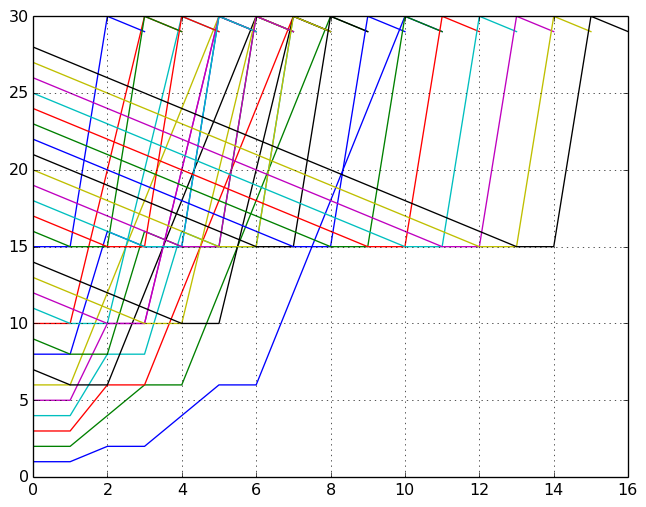
N=29:
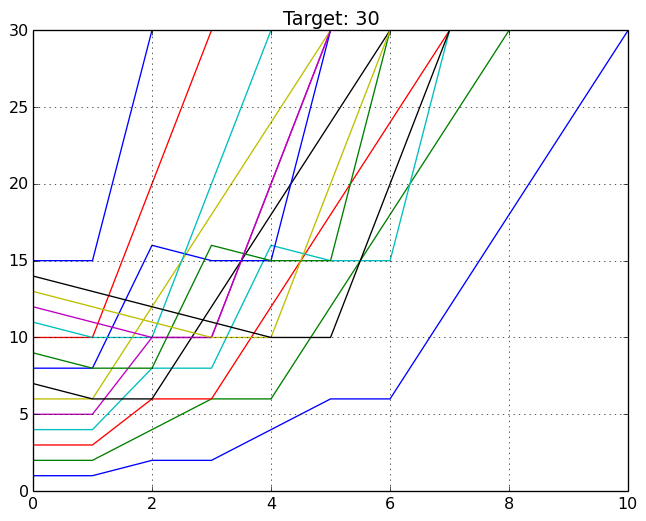
N=30:
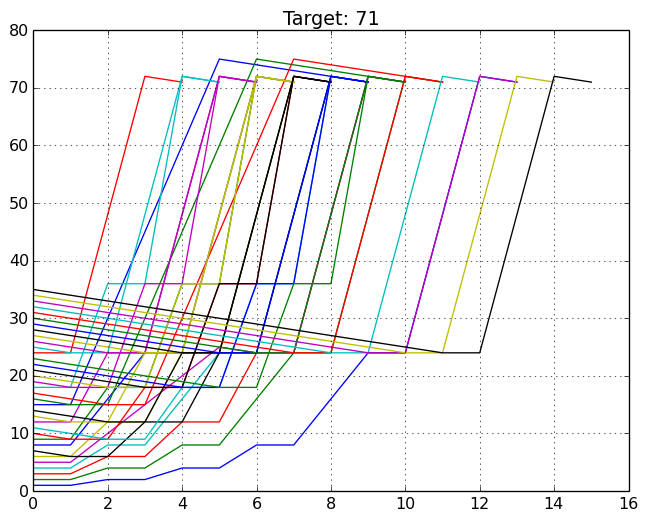
N=71:
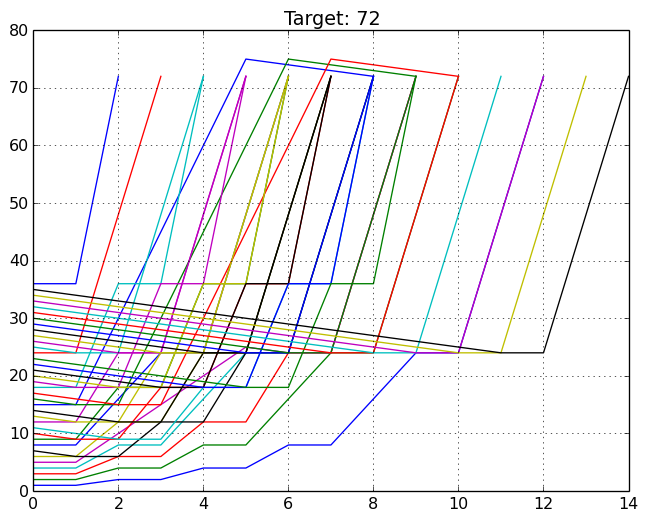
N=72:
PDF со всеми картинками:
dugin.org/dropbox/toster_188303.pdf (11 Mb)
P.S.
https://ru.wikipedia.org/wiki/Задача_о_ранце 





