Почему именно синус?

Question

[Urukhayy]

Доброго времени суток. Есть такая задачка:
На плоскости есть точка. Мы знаем куда это точка "смотрит", то есть знаем её градус поворота. Если у нас есть градусы поворота, стало быть у нас мысленная окружность. Так вот, требуется определить координаты второй точки, которая находится всегда там, куда "смотрит" наша первая точка. То есть если первая точка смотрит на 30 градусов, то надо узнать координаты той точки, которая находится по этим 30 градусам. Вот рисунок:



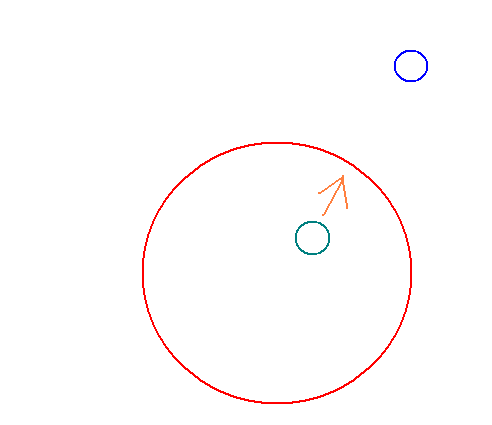
Зеленый круг - исходная точка. Мы знаем её координаты X,Y и угол поворота, то есть куда она смотрит (показано стрелкой).
Нам нужно найти координаты синей окружности (она всегда там, куда смотрит зелёная окружность, и отдалено от неё на 10 координат).

А теперь почему я в вопросе упомянул синус. Дело в том, что я встречал решение данной задачи, но не совсем понял, почему оси X прибавляли sin угла умноженный на 10, а оси Y cos, тоже умноженный на 10.

Comments

[krypt3r]

и отдалено от неё на 10 координат

Как понять эту фразу? {x2 = 10 * x1; y2 = 10 * y1}?

[Urukhayy]

krypt3r: Значит что между ними по прямой всегда 10 координат. В Вашем примере не задействован поворот. Мне нужно получать координаты только там, куда смотрит первая точка, да еще и на расстоянии 10 координат по прямой.

Answer 1

[Vit]

Это прямо следует из определения синуса и косинуса. sin(x) - ордината точки единичной окружности с дугой угла x, cos(x) - абсцисса.

Comments

[Urukhayy]

Отличный рисунок, за этой прям лайк) Но всё-же, почему в том решении к Y прибавляли косинус, а не синус? Синус же параллелен Y..

[Vit]

Urukhayy: вы слишком туманно ваше решение описали. Приведите четкие формулы, тогда возможно я смогу ответить.

[Mrrl]

Urukhayy: Вероятно, там угол отсчитывался от оси Y по часовой стрелке - как на компасе или циферблате часов.

[Urukhayy]

Mrrl: Да, от оси Y, но против часовой стрелки)

[Vit]

Urukhayy: это все и объясняет. Сдвиг на pi/2 превращает синус в косинус и наоборот.

[Mrrl]

Urukhayy: Если от оси Y против часовой стрелки, то от x надо отнимать синус, а не прибавлять его.

[Urukhayy]

Mrrl: Да, а можно к вектору прибавить 90 градусов.

Answer 2

[Mrrl]

В этой задаче синус не нужен.

double r=sqrt(x*x+y*y);
double cf=1+10/r;
double x1=x*cf,y1=y*cf;

(x1,y1) - координаты искомой точки.

Comments

[Urukhayy]

Как Вы нашли поворот без синуса? Вот решение:
x2 = x1 + distance * cos(vector);
y2 = y1 + distance * sin(vector);

[Mrrl]

Urukhayy: Так что у вас на входе: x1,y1 (в ваших терминах) или vector?

[Mrrl]

Urukhayy: А, ясно. Меня смутила красная окружность. Я думал, что точка "смотрит" в направлении от центра этой окружности (как будто это зрачок глаза).

Answer 3

[ThemeZV]

Напомню, что sin - отношение противолежащего катета к гипотенузе, cos - отношение прилежащего катета к гипотенузе.