Определение положения точки с максимальным весом

Question

[Explode]

Есть координатная плоскость. На ней расположено несколько точек, каждая из которых имеет свой вес (от 0 до 99). Известны их координаты и значение веса. Так же известен тот факт, что в центре всех этих точек находится одна точка с весом 100, но ее координаты не известны. Чем остальные точки находятся дальше от нее, тем меньше их вес.
Вот нужно как нибудь по нескольким точкам определить положение точки с максимальным весом.

Подобные алгоритмы реализованы в программах определения координат Wi-Fi роутеров по анализу сигнала на близлежащей территории.

Answer 1

[vare6gin]

В случае, если зависимость между координатами и весом точки, например, линейная, то нужно решить уравнение: w=a*x + b*y + c. Для этого необходимы 3 точки.

После решения (найдены a, b и c) можно выразить уравнение прямой, для которой w=100:
y=(100 — a*x — c)/b.

Далее необходимо решить w=a'*x + b'*y + c' относительно другой комбинации точек.

Искомой точкой с весом 100 будет пересечением y=(100 — a*x — c)/b и y=(100 — a'x — c')/b'.

Повторюсь, что это решение для линейной зависимости между координатами и весом. Если я сделал ошибку в рассуждениях (а это очень вероятно, так как матан очень давно был), то напишите где.

Спасибо.

Comments

[vare6gin]

Для экспериментальных данных, в которых присутствует случайная составляющая, выраженные прямые будут пересекаться в нескольких точках. В этом случае, можно найти центр масс фигуры из точек пересечений прямых.

Answer 2

[Eddy_Em]

Если точек достаточно много, можно построить изолинии веса и определить положение центра по скелетам изообластей.

Answer 3

[Алексей]

Определять удаленность точки от центра. По двум точкам можно найти 2 возможных варианта, третья укажет какая именно из двух точек пересечения окружностей будет центром.
Тут, соответственно, по координатам. Можно составить уравнения окружности для точек.

Answer 4

[VasG]

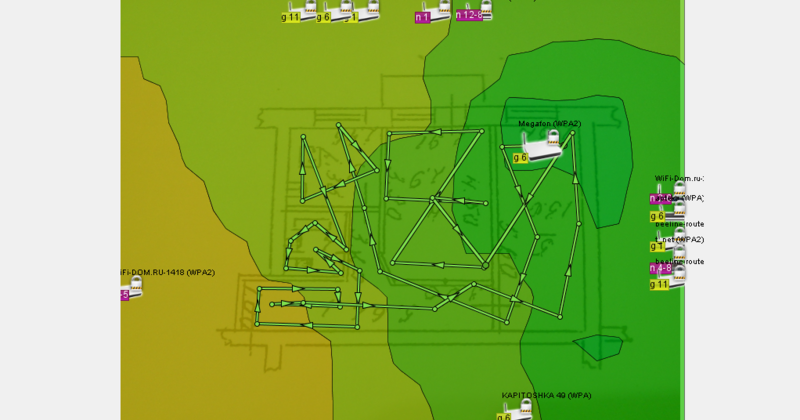
Можно брать точки попарно и строить на их основе векторы. Чем больше разница в весе точек, тем больше «длина» вектора, их соединяющего, направление определяется точкой с наибольшим весом.

По идее, если провести из одной точки два подобных вектора, угол между которыми будет >=Pi/2, то существует вероятность («вероятность» потому, что я просто не уверен. Мой внутренний голос подсказывает, что так должно быть в 99% сулчаев) того, что вертор, полученный суммированием предыдущих двух укажет направление в сторону точки с наибольшим весом.


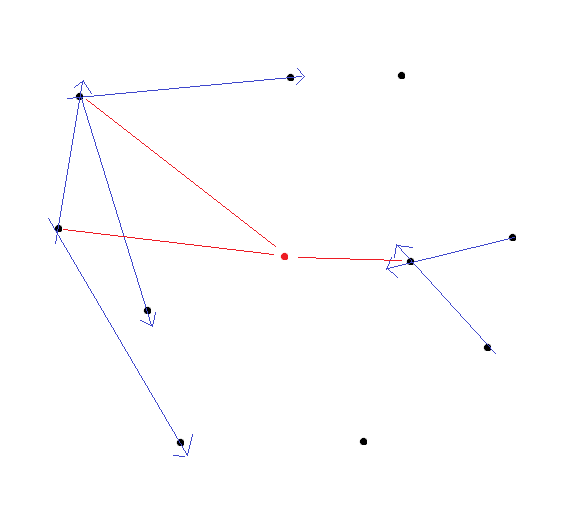
Далее нужно продлить полученные вектора до прямых, и найти точку их пересечения. Точка, в которой пересекается наибольшее количество прямых — искомая (как искать точку с наибольшим количеством пересечений я упомянул в своей статье).

Comments

[VasG]

Хотя про Pi/2 что-то я перемудрил, кажется.

[Explode]

А можно подробнее, что на счет pi/2 не так?

Answer 5

[AlexanderG]

Можно попробовать триангуляцию. Для начала определим (произвольно) соответствие веса и радиуса окружности (потребуется позже). Затем берем три точки, строим для них окружности соответствущих их весам радиусов, получаем область, ограниченную точками пересечения окружностей. Далее увеличиваем/уменьшаем радиусы окружностей, стремясь уменьшить площадь ограниченной точками пересечения области. В конечном счете эта область выродится в точку, которая и будет искомым центром.

Answer 6

[Mrrl]

Метод наименьших квадратов. Если расстояние от искомой точки (x,y) до одной из известных (xi,yi) равно ri, то (x-xi)^2+(y-yi)^2-ri^2=0 (с точностью до шума). Строим f(x,y)=Sum(((x-xi)^2+(y-yi)^2-ri^2)^2) (это многочлен 4-й степени от двух переменных), и решаем систему уравнений {df/dx=0, df/dy=0} например, методом Ньютона. Но не факт, что корень будет единственным, так что надо пробовать много стартовых точек, и для каждого результата проверять значение f.

Comments

[Mrrl]

Лучше даже суммировать (((x-xi)^2+(y-yi)^2)/ri^2-1)^2. А если мощность источника неизвестна — добавить еще один параметр: (((x-xi)^2+(y-yi)^2)/ri^2-w)^2

Answer 7

[EndUser]

Не могу сообразить как решать ситуацию 60-90 (точки на одной линии):
а)!60!-(70)-(80)-!90!-! он!
б)!60!-(70)-(80)-(90)-! он!-!90!
!!! обозначена реальная точка
() обозначена виртуальная (расчётный вес на расстоянии)
он искомый рутер
Пока что напрашивается требование по жёсткой зависимости веса по расстоянию — если жёсткой нет, то задача не решаема, ИМХО

Answer 8

[Explode]

Вот к примеру результат работы программы Ekahau HeatMapper. На картинке изображена еще «тепловая карта» мощности сигнала. Как можно заметить, жесткой зависимости нет — «поле» не имеет формы круга, однако местоположение исследуемой точки (Megafon) и других соседних определилось довольно точно.

Точки, которые соединяют линии, можно считать нашими точками, у которых известны вес и координаты.