Как определить ближайших соседей прямоугольника с заданной стороны на поле с пропусками, без полного перебора?

Question

[makaleks]

Пусть задан одномерный массив прямоугольников, они могут касаться друг-друга, могут нет. Пересечений нет. Порядок прямоугольников следует интуитивному алгоритму: по возрастанию с приоритетом оси Y больше X, начало координат сверху слева, область видимости ограничена сверху и снизу - то есть прямоугольники лежат как-бы построчно. 'Сетки' нет, координаты вещественные. Поиск остановить, как только найдены все соседи, перекрывающие целевую сторону.

Сабж в теме. Дополняю формулировку примером с иллюстрации:



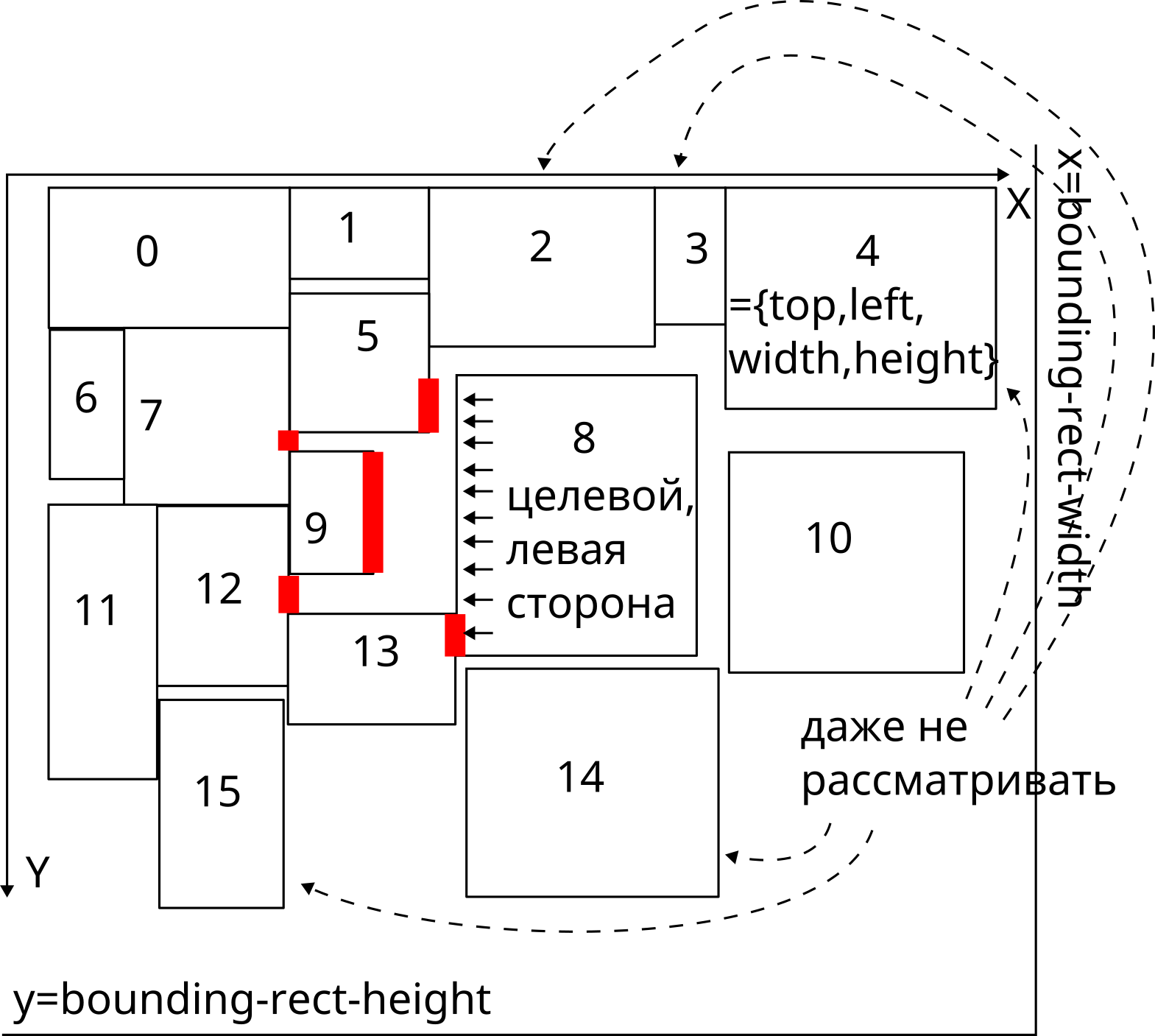
На рисунке разыскиваются соседи восьмого прямоугольника по левой стороне. Это должны быть прямоугольники 5,7,9,12,13. Прямоугольники дальше/раньше даже не рассматривать, что визуально кажется очевидным.

Какие мысли:
1. надо рассматривать каждую отдельную сторону, и делать от целевого прямоугольника некоторое количество шагов по массиву вперёд и/или назад - алгоритм кажется плюс-минус одинаков
2. вроде как нужен счётчик по стороне в виде вектора

[{rect_idx, {side_segment_used_p1, side_segment_used_p2}}]

, так можно будет остановиться по достижении 'конца' и не учитывать прямоугольники, которые не деляют вклада в этот счётчик (в 'красные линии' на иллюстрации)
3. сортировку прямоугольников (построчное размещение) я уже ввёл, без неё совсем мрак

Где-то тут и застрял. Кажется многовато выходит сущностей. А ведь нужен ещё какой-то учёт ситуации, когда 'вклад в сторону' делает не сосед-прямоугольник, а ось координат (стенка). Строгая формулировка критерия остановки. Может ещё что-то. Идеально, если это решённая задача, которую я просто не осилил нагуглить.

Спасибо!

Comments

[mayton2019]

А где твой исходник? Или ты на бумаге программируешь?

[makaleks]

mayton2019, по-моему он несъедобен

но вот

pub type SinglePrecision = f32;
pub type DoublePrecision = f64;

#[derive(Debug, Clone, Copy)]
pub struct Size2D {
    pub width:  SinglePrecision,
    pub height: SinglePrecision,
}
// coordinates are assumed to start from top-left corner
#[derive(Debug, Clone, Copy)]
pub struct Position2D {
    pub top:  SinglePrecision,
    pub left: SinglePrecision,
}
#[derive(Debug, Clone, Copy)]
struct Segment2D {
    // {y2,x2} >= {y1,x1}
    p1: Position2D,
    p2: Position2D,
}
impl Segment2D {
    fn new (p1: Position2D, p2: Position2D) -> Self {
        let mut array = [p1, p2];
        array.sort_by(
            |p1, p2|
            p1.top.partial_cmp(&p2.top).unwrap()
                .then(p1.left.partial_cmp(&p2.left).unwrap())
            );
        Self {p1: array[0], p2: array[1]}
    }
}
#[derive(Debug, Clone, Copy)]
pub struct BoundingRect2D {
    pub size:     Size2D,
    pub position: Position2D,
}
impl BoundingRect2D {
    fn from_size_at_0 (size: Size2D) -> Self {
        Self {size, position: Position2D {top: 0., left: 0.}}
    }
    fn height (&self) -> SinglePrecision {
        self.size.height
    }
    fn left (&self) -> SinglePrecision {
        self.position.left
    }
    fn right (&self) -> SinglePrecision {
        self.position.left + self.size.width
    }
    fn top (&self) -> SinglePrecision {
        self.position.top
    }
    fn bottom (&self) -> SinglePrecision {
        self.position.top + self.size.height
    }
    fn left_top (&self) -> Position2D {
        Position2D{top: self.top(), left: self.left()}
    }
    fn right_top (&self) -> Position2D {
        Position2D{top: self.top(), left: self.right()}
    }
    fn left_bottom (&self) -> Position2D {
        Position2D{top: self.bottom(), left: self.left()}
    }
    fn right_bottom (&self) -> Position2D {
        Position2D{top: self.bottom(), left: self.right()}
    }
    fn does_x_intersect_with (&self, left: SinglePrecision, right: SinglePrecision) -> bool {
        // !((a.max < b.min) || (b.max < a.min))
        !((right <= self.left()) || (self.right() <= left))
    }
}

trait MyAverage1
{
    type Output;
    fn my_average (self) -> Self::Output;
}
trait MyAverage2
{
    type Output;
    fn my_average (self) -> Self::Output;
}
impl<T> MyAverage1 for T
where T: Iterator<Item=SinglePrecision>
{
    type Output = DoublePrecision;
    fn my_average (self) -> Self::Output {
        let (mut total, mut count) = (DoublePrecision::from(0u8), DoublePrecision::from(0u8));
        for v in self {
            total += DoublePrecision::from(v);
            count += DoublePrecision::from(1u8);
        }
        total / count
    }
}
impl<T> MyAverage2 for T
where T: Iterator<Item=(SinglePrecision, SinglePrecision)>
{
    type Output = (DoublePrecision, DoublePrecision);
    fn my_average (self) -> Self::Output {
        let (mut total, mut count) = ((DoublePrecision::from(0u8), DoublePrecision::from(0u8)), DoublePrecision::from(0u8));
        for v in self {
            total.0 += DoublePrecision::from(v.0);
            total.1 += DoublePrecision::from(v.1);
            count += DoublePrecision::from(1u8);
        }
        (total.0 / count, total.1 / count)
    }
}

fn gen_initial_size_for_undefined<It: Iterator<Item=Option<Size2D>>> (sizes_opt_it: It, minimal_rect_size: Size2D) -> Size2D
{
    let (avg_width, avg_height)
        = sizes_opt_it
          .filter_map(
              |size_opt|
               size_opt.map(|size| (size.width, size.height))
              )
          .my_average();
    let middle_or
        = |middle: DoublePrecision, minimal: SinglePrecision|
          if middle < minimal.into() {minimal} else {middle as SinglePrecision};
    Size2D {
        width:  middle_or(avg_width, minimal_rect_size.width),
        height: middle_or(avg_height, minimal_rect_size.height),
    }
}

fn get_min_and_premin_for<T: PartialOrd + Copy, It: Iterator<Item=T>> (mut it: It) -> Option<((usize, T), Option<(usize, T)>)> {
    let mut min_idx_and_value = match it.next() {
                                    None    => return None,
                                    Some(v) => (0, v),
                                };
    let mut pre_min_idx_and_value = None;

    let mut it = it.enumerate().map(|(idx, v)| (1 + idx, v));
    while let Some((i, v)) =  it.next() {
        if v < min_idx_and_value.1 {
            pre_min_idx_and_value = Some(min_idx_and_value);
            min_idx_and_value = (i, v);
        }
    }

    Some((min_idx_and_value, pre_min_idx_and_value))
}

struct Step {
    value:         DoublePrecision,
    sourse:        *const InteractableBoundingRect2D,
    relative_size: SinglePrecision,
}

struct InteractableBoundingRect2D {
    bounding_rect: BoundingRect2D,
    top_steps:     Vec<Step>,
    bottom_steps:  Vec<Step>,
    left_steps:    Vec<Step>,
    right_steps:   Vec<Step>,
}

fn make_bounding_rects_interactable (rects: Vec<BoundingRect2D>) -> Vec<InteractableBoundingRect2D> {
    rects.into_iter().map(
        |bounding_rect|
        InteractableBoundingRect2D {
            bounding_rect,
            top_steps: Vec::new(),
            bottom_steps: Vec::new(),
            left_steps: Vec::new(),
            right_steps: Vec::new()
            }
        ).collect()
}

#[derive(Debug, Clone, Copy)]
enum Direction {
    Top,
    Bottom,
    Left,
    Right,
}
impl Direction {
    fn into_reverse (self) -> Self {
        match self {
            Self::Top    => Self::Bottom,
            Self::Bottom => Self::Top,
            Self::Left   => Self::Right,
            Self::Right  => Self::Left,
        }
    }
}
#[derive(Debug, Clone, Copy, Default)]
struct Segment1D {
    // p2 >= p1
    p1: SinglePrecision,
    p2: SinglePrecision,
}
impl Segment1D {
    fn new (p1: SinglePrecision, p2: SinglePrecision) -> Self {
        let mut array = [p1, p2];
        array.sort_by(|p1, p2| p1.partial_cmp(p2).unwrap());
        Self {p1: array[0], p2: array[1]}
    }
    fn from_bounding_rect_side (br: BoundingRect2D, direction: Direction) -> Self {
        match direction {
            Direction::Top | Direction::Bottom => Self {p1: br.left(), p2: br.right()},
            Direction::Left | Direction::Right => Self {p1: br.top(), p2: br.bottom()},
        }
    }
    fn from_bounding_rect_side_reverse (br: BoundingRect2D, direction: Direction) -> Self {
        Self::from_bounding_rect_side(br, direction.into_reverse())
    }
    fn does_intersect_with (&self, other: Self) -> bool {
        // !((a.max < b.min) || (b.max < a.min))
        !((self.p2 <= other.p1) || (other.p2 <= self.p1))
    }
}

struct Segment1DSideCollection {
    from:              SinglePrecision,
    to:                SinglePrecision,
    used_rect_idx_acc: Vec<(usize, Segment1D)>,
    direction:         Direction,
}
impl Segment1DSideCollection {
    fn new_empty () -> Self {
        Self {from: 0., to: 0., used_rect_idx_acc: Vec::new(), direction: Direction::Top}
    }
    fn reset (&mut self, from: SinglePrecision, to: SinglePrecision, direction: Direction) {
        self.used_rect_idx_acc.clear();
        (self.from, self.to, self.direction) = (from, to, direction);
    }
    fn get_new_part_opt (&self, next_segment: Segment1D) -> Option<Segment1D> {
        self.used_rect_idx_acc.iter().position(|(_, existing)| existing.does_intersect_with(next_segment)).is_some()
    }
    fn try_next_down<It: Iterator<Item=(usize, Segment1D)>> (&mut self, it: It) -> Option<It> {
        while let Some((usize, segment)) = it.next() {
        }
        None
    }

    fn try_next<Map: Fn(&BoundingRect2D)->SinglePrecision, Filter: Fn(&BoundingRect2D,&Self)->bool> (&mut self, for_segment: Segment2D, next_i: usize, rects: &Vec<InteractableBoundingRect2D>) -> Option<usize> {
    }
    fn is_next_reasonable (&mut self, next_i: usize, rects: &mut Vec<InteractableBoundingRect2D>, direction: Direction) {
    }
    fn get_rects_new (&mut self, from_idx: usize, rects: &mut Vec<InteractableBoundingRect2D>, direction: Direction) -> Vec<&mut InteractableBoundingRect2D> {
        self.reinit(rects[from_idx].bounding_rect, direction);
        let mut result = Vec::new();
        result
    }
    fn get_rects_left (&mut self, from_idx: usize, rects: &mut Vec<InteractableBoundingRect2D>) -> Vec<&mut InteractableBoundingRect2D> {
        self.get_rects_new(from_idx, rects, Direction::Top)
    }
}

fn get_rects_left (from_idx: usize, rects: &mut Vec<InteractableBoundingRect2D>) -> Vec<&mut InteractableBoundingRect2D> {
}
fn get_rects_right (from_idx: usize, rects: &mut Vec<InteractableBoundingRect2D>) -> Vec<&mut InteractableBoundingRect2D> {
}
fn get_rects_top (from_idx: usize, rects: &mut Vec<InteractableBoundingRect2D>) -> Vec<&mut InteractableBoundingRect2D> {
}
fn get_rects_bottom (from_idx: usize, rects: &mut Vec<InteractableBoundingRect2D>) -> Vec<&mut InteractableBoundingRect2D> {
}

что-то не хочет подсвечивать явно указанный язык

[mayton2019]

Данная задача очень похожа на гео-поиск. Там вроде бы используют R-Tree, Quad-Tree индексы.
Почитай. Хотя я не уверен что тебе обязательно решать эту задачу через пространственные индексы.

Если задача одноразовая и нужно только отдавать быстрые ответы - то попробуй для каждого прямоугольника
явно хранить списки "леваков". Тогда мы уходим от полного перебора но нам нужна долгая инициализация всех
структур.

Если эта задача является подзадачей чего-то более крупного (оптимальный раскрой например) - то тут уже надо
думать дальше.

[Wataru]

mayton2019, можно всех соседей за n log n найти.

[mayton2019]

Wataru, я все еще считаю что это часть другого алгоритма. Поэтому завязываться на отрезки еще не хочется.

[Alexandroppolus]

Набор прямоугольников неизменен? Т.е. могут ли запросы на изменение набора идти вперемешку с запросами на соседей некоторого прямоугольника?

[makaleks]

Alexandroppolus, да, неизменен

Answer 1

[Wataru]

Эта задача решается алгоритмом "сканирующая прямая".

Представьте что у есть вертикальная линия, которая двигатеся слева-направо непрерывно. В каждый момент времени на прямой могут появиться какие-то прямоугольники, могут закончиться какие-то прямоугольники или ничего не поменяется - в этот момент прямая какие-то прямоугольники пересекает.

Надо взять какую-то хитрую структуру данных, чтобы хранить все открытые (в данном случае - последние закрытые) прямоугольники на прямой. В моменты открытия/закрытия прямоугольников надо структуру данных обновлять или опрашивать.

Тут подойдет что-нибудь вроде std::set в C++ - структура хранящая упорядоченное множество объектов, с доступом и изменением за логарифм, умеющая искать ближайший к заданному значению слева и справа (lower_bound, upper_bound). Хранить в ней мы будем вертикальные отрезки, помеченные номерами их прямоугольникв. Не знаю ее аналоги в других языках - нужно что-то реализованное или на binary search tree, или на skip list.

Когда прямоугольник открывается надо посмотреть, с какими отрезками в set данный отрезок пересекается. Все эти отрезки надо добавить в ответ, удалить полностью покрываемые новым отрезком, а торчащие из него укоротить. Таким образом мы будем поддерживать множество "видимых" отрезков с прямой - ближайших к ней слева.

В этой задаче можно забить на правые границы прямоугольников и на их ширину (раз нет пересечений). Соседями каждого отрезка - левого края будут ближайшие к нему левые края каких-то прямоугольников.
Поэтому вам надо получить все отрезки заданные в виде {x, y1, y2, id} и отсортировать их (сначала по x, потом по y). Потом в этом порядке их обходите и применяйте новый отрезок к структуре данных. Все удаляемые отрезки + 2 пересекающихся сверху и снизу пойдут в список соседних для нового отрезка.

Этот алгоритм за O(n log n) получит всех соседей для всех прямоугольников.
Это что-то похожее вот на эту задачку с leetcode

Comments

[Alexandroppolus]

отсортировать их (сначала по x, потом по y)

по У необязательно

удалить полностью покрываемые новым отрезком, а торчащие из него укоротить

ещё может понадобится разрезать на два отрезка.
например, очередной отрезок - {1, 2, 3, id2}, а слева от него - {0, 1, 4, id1},
тогда последний надо разрезать на {0, 1, 1, id1} и {0, 3, 4, id1}, т.е. исходный укоротить, и один добавить. Появляются несколько одинаковых id, и если в списке соседей id не должны дублироваться, то это надо проверять.

[Wataru]

Alexandroppolus, да, вы правы.