Простите что длинный вопрос, но для полного понимания сути я с начало описал свои знания, потом задал основные вопросы, они пронумерованы
В общем начал просматривать тему структуры данных и узнал вот что
а)стек,дек и очередь это просто встроенный список (list)с которым мы работаем с определенной последовательностью, хотя можно использовать не только список, а экземпляр класса или модуль
б)Связанный список это тоже список, но из за того что встроенный список устроен для некоторых задач не разумно, я про вставку в начало, то связанный список лишен этих проблем
важно, связанный список очевидно отличается от встроенного списка, и реализуется как экземпляр класса, где узел содержит ссылку на следующий узел
в)так же узнал что
дек разумно написать как связанный список, и по сути это двусвязный список,
эта логика мне тоже понятна, надо вставлять узел в начало эффективно))
г)Графы, терминология и задачи графа вполне понятны, реализация очень интересна, это
- список смежностей
- список ребер
- матрица смежностей
- матрица ребер, возможно термин не верен
д)Деревья
а вот тут уже есть вопросы которые не получается осмыслить в интернете, к примеру
1) пишут что дерево это граф без цикла, это понятно, но значит ли что дерево можно представить как
- список смежностей
- список ребер
- матрица смежностей
- матрица ребер, возможно термин не верен
и если можно, то имеет ли это смысл? делает так кто нибуть?
2)так же в википедии есть такая картинка
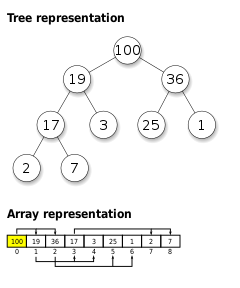
здесь показано что дерево можно представить в виде встроенного списка, но примеры реализации такого подхода я не нашёл, так вообще делают?
3)Находил пример где Дерево реализуют на подобии связанного списка, значит ли что дерево это тоже просто список? потому что Дерево хоть и похоже на граф, но вершины графа имеют пространственную логику, а у дерева вершины это причинно следственная последовательность и иерархия, из за чего дерево больше похож на связанный список, это так?
4)так же прочитал что
Зачем нужны деревья
Другие структуры данных, например, массивы, списки, стеки и очереди, линейные. Это значит, что данные в них хранятся последовательно. Когда мы выполняем любую операцию в линейной структуре данных, временная сложность растет с увеличением размера данных. В современном мире это не очень круто.
Разные древовидные структуры позволяют быстрее и легче получать доступ к данным, поскольку дерево — структура нелинейная
значит дерево это просто список для более быстрого поиска?
5)с учётом всего выше сказанного, я пока сделал вывод что дерево это одна из реализаций связанного списка, хотя об этом ни кто не говорит, я понимаю что можно и в виде
встроенного списка представить дерево или например в виде
словаря, но как это делают в реальных задачах?
