Многие из хабравчан были на конференции Яндекса YAC2011. Многие из тех, кто там был, видели площадку школы Яндекса и наверняка пробовали решать задачки. Я тоже пробовал. Причём пробовал очень долго. Решение, которое удовлетворило бы представителей школы Яндекса я так и не нашёл, поэтому решил обратиться за помощью к хабрасообществу.
Задача звучит так: "
Приведите пример графа, в котором степени всех вершин равны 3, но нельзя разбить вершины на пары смежных".
Своё первое решение я сделал минут за 5. Выглядело оно так:
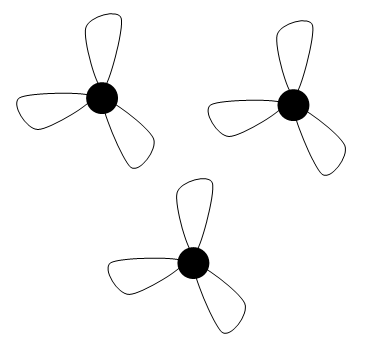
Разумеется, можно было бы обойтись и одной вершиной вместо трёх, но тогда я об этом не подумал.
Странно другое мне сказали, что моё решение неправильное. Более того, мне сказали, что то, что я нарисовал, не является графом. Я посидел там ещё около часа, пытаясь решить эту задачку, так ни до чего не додумался, и поехал на работу.
Приехав домой, я полез в учебники. Оказывается, что граф это тройка Г=(X,U, Ф), где X — конечное множество вершин; U — конечное множество дуг; Ф — трёхместное отношение инцидентности Ф(x,u,y), где x,y — элементы множества X, u — элемент множества U. Кроме того на Ф накладывается два условия: 1. Ребро всегда соединяет пару вершин; 2. Ребро соответствует не более чем одной паре вершин.
Вопрос мой заключается вот в чём:
1. Неужели моё решение и правда неправильное?
2. Если оно неправильное, то как выглядит правильное решение?


