Как получить минимальную рамку кривого контура по границам контура?

Question

[SergeySerge11]

Вот есть контур, я легко могу составить прямоугольную вертикальную рамку.(вторая) но она не оптимальная может быть в многих случаях Площадь будет больше. Тогда как можно сделать повернутую с меньшей площадью. Есть алгоритмы оптимальные. На вход поступают вершины всех точек кривой.

Comments

[Армянское Радио]

В качестве идеи - найти координаты центра тяжести, сдвинуть так, чтобы начало координат попало в центр тяжести.
Линейной регрессией определить наклон
Развернуть систему координат относительно начала координат так, чтобы прямая, полученная в результате выполения линейной регресии стала одной из осей.
Найти координаты углов как минимумы и максимумы точек в новой системе координат

Answer 1

[Wataru]

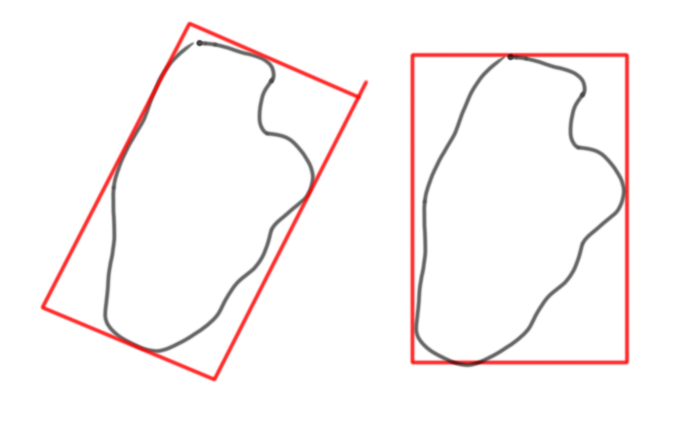
Есть алгоритм за O(n log n), где n - количество точек в кривой.

Во-первых, можно достроить кривую до выпуклой оболочки. Получится выпуклый многоугольник. Описанная вокруг кривой рамка будет описаной и вокруг выпуклой оболочки. Алгоритмы есть, например, на хабре, или вот есть с реализацией.

Во-вторых, можно доказать (смотрите комментарии к этому ответу, спасибо Alexandroppolus за идею), что рамка обязательно проходит через хотябы сторону выпуклой оболочки. Иначе ее можно вращать, уменьшая площадь пока она не коснется стороны.

Далее, если рамку чуть-чуть вращать, то точки касания или не поменяются вообще, или перейдут на слудующую вершину в выпуклой оболочке. Поэтому можно найти четыре точки касания для вертикально-горизонтальной рамки просто перебрав все вершины выпуклого многугольника, а дальше вместо перебора можно просто смотреть, а не надо ли сдвигать какие-то точки касания вперед.

Удобно это реализовывать, если взять углы наклона всех сторон оболочки, их же сдвинутые на 90, 180 и 270 градусов и отсортировать. Далее надо перебирать рамки с такими углами наклона певрой стороны (можно в пределах [0,90) градусов). Первую рамку найдите перебором, а дальше какие-то точки надо будет сдвигать.

Итак, весь алгоритм:
1) построить выпуклую оболочку
2) добавить в массив углы всех сторон и их копии повернутые на 90, 180 и 270 градусов и отсортировать, но не добавлять углы не в [0,90).
3) для первого угла в массиве найдите 4 точки касания рамки.
4) Для каждого отрезка углов в отсортированном массиве проверить, а надо ли сдвинуть точки касания вперед (каждую из четырех точек со своим углом), потом найти площадь рамки в известных точках с известным наклоном.

Вместо работы с углами, для чего нужны тригонометрические функции, можно работать с векторами на единичной окружности. На отрезке углов можно легко взять середину, просто сложив два вектора-границы и нормировав. Для тернарного поиска не обязательно брать 1/3 и 2/3 на отрезке, поэтому можно так же просто просуммировать вектора с коэффициентами 1 и 2 и опять нормировать (v1+2*v2). Сортировать по углу тоже можно сравнивая вектора через векторное произведение векторов (иногда его называют псевдоскалярным).

Чтобы найти рамку с заданным углом на точках не надо ничего пересекать (кроме ответа в конце, если вам надо координаты рамки вывести, а не только площадь найти). Надо представить прямые в виде cosa*x + sina*y + c = 0. Отсюда, зная точку (x, y) и угол прямой (a), можно найти c. cosa и sina считать не надо - это координаты вектора, перпендикулярного к известному вектору наклона прямой. Когда вы нашли два значения c для двух параллельных сторон, эти коэффициенты можно сложить - это и будет расстояние между сторонами (надо складывать, потому что cosa и sina в этих двух прямых будут с разными знаками, ведь у одной прямой угол на пол оборота больше). Остается подсчитать это два раза для перпендикулярных прямых и перемножить.

Код для пересечения прямых в конце можно посмотреть тут.

Comments

[Alexandroppolus]

есть сильное подозрение, что на границе искомого прямоугольника обязательно будет лежать не 4, а как минимум 5 вершин выпуклой оболочки (то есть хотя бы одна из её сторон), если конечно в ней более 4 вершин. Потому, имея список вершины выпуклой оболочки, так что они сортированы в порядке обхода, можно проверить все прямые, проходящие через каждую сторону, и для каждой такой определить площадь, вычислив 3 другие стороны прямоугольника. Эти 3 стороны можно поворачивать синхронно и потому вычислять за О(1), Закончить обход, когда повернёмся на 90 гр.

[Wataru]

Alexandroppolus, Если можно доказать, что ответ точно проходит через сторону, то да, можно без троичного поиска - достаточно проверить только углы вдоль сторон оболочки (и повернутые на 90, 180, 270) градусов.

Я пока не нашел контр-примера, но и доказать это я не могу.

Про поиск сделующих точек касания при сдвиге за O(1) я написал.

[ambisinister One]

Wataru, Я сначала подумал, что тут площадь трёхмерной двояковыпуклой хитрой
фигуры вычисляется... У вас тут все так сложно считают? Немного знаком с математикой.
Столько слов и информации для описания плоской неровной поверхности?

[Alexandroppolus]

Wataru, идеи по доказательству.

Рассмотрим рамку, которая не проходит через сторону выпуклой оболочки. На рисунке синии линии соединяют точки касания.



С первой картинкой всё просто - если повернуть рамку по часовой стрелке, то уменьшатся и высота и ширина. То есть это явно не минимум.

Вторая рамка хитрее - там при повороте одно растет, другое уменьшается, и что с площадью, не сразу понятно.

Высота рамки равна H, ширина W.
Допустим, при повороте рамки на очень маленький угол A против часовой стрелки высота уменьшилась на h1, ширина увеличилась на w1, площадь при этом уменьшилась на s1 = (W*h1 - H*w1 + h1*w1). Если ещё раз повернуть на угол А, то легко можно показать, что w2 < w1, h2 > h1, и новое уменьшение s2 будет ещё больше, чем s1. То есть чем дальше крутим, тем выгоднее, и так до касания одной из сторон оболочки.

Теперь допустим, что у нас изначально была минимальная рамка, и поворот на угол А в любом направлении увеличивает площадь. Тогда повернем на А по часовой стрелке, увеличив площадь. Теперь если обратно повернуть на А против часовой, площадь уменьшится, но по доказанному ранее, тогда ещё один поворот против часовой должен ещё уменьшить площадь.

Таким образом, минимальная рамка не может проходить только через точки.

[Wataru]

ambisinister One, Ну что поделать, алгоритм сложный. В принципе, если опустить объяснение, почему это работает, да пару абзацев советов по реализации, то можно раза в 2 сократить текст. Но мне же непонятен уровень собеседника, поэтому расписывал детально.

[Wataru]

Alexandroppolus,

Если ещё раз повернуть на угол А, то легко можно показать, что w2 < w1, h2 >

Вот это непонятно.

Но я по-другому доказал.

Обозначте острый угол между синей прямой и вертикальной стороной x. Площадь рамки пропорциональна sin(x)cos(c-x), где c - острый угол между синими прямыми.

Ширина рамки пропорциональна sin(x) - если провести горизонтальную высоту из левой вершины, то в прямоугольном треугольнике против угла x лежит ширина рамки. Вот и синус. Теперь надо найти острый угол между второй синей прямой и горизонтальной стороной рамки. Ясно, что этот угол будет в форме a-x. потому что поворот рамки увеличивает один острый угол и уменьшает второй. Из правого верхнего четырехугольника можно составить уравнение 360=c+(180-x)+90+(180+x-a). Отсюда a=c+90. Т.е. высота рамки пропорциональна sin(c+90-x) = cos(c-x).

Итак, площадь равна константе (длины синих отрезков) умноженной на sin(x)cos(c-x). Возьмем производную. Можно упростить как косинус разности. В итоге производная: cos(c-2x). Она равна нулю при с-2x = -90. Берем -90, потому что -180 < с-2x < 90, ведь 0 < c, x < 90. Т.е. точка экстремума вполне себе есть. Но может ли она быть минимумом? Вторая производная - 2sin(c-2x). Но мы помним, что с-2x=-90, а значит вторая производная отрицательна, а значит эта единственная точка экстремума - максимум.

[Alexandroppolus]

Wataru,

Вот это непонятно.

напомню, что w2 и w1 - это изменение ширины при изменении угла, а не ширина. По сути, это производная dW/dA. То есть, в моем примере, если ширина пропорциональна sin(x), то w2 и w1 пропорциональны cos(x). Вращая рамку против часовой стрелки, увеличиваем этот угол к 90 градусам, косинус уменьшается.

Answer 2

[U235U235]

Откройте исходники OpenCV и посмотрите как это сделано в функции minAreaRect. Все.

Comments

[Wataru]

Вот код. Правда по нему не так просто разобраться. Но на самом деле - там в точности описанный мной алгоритм.

Answer 3

[profesor08]

Найди самые дальние, друг от друга, точки, проведи между ними мнимую прямую. Потом найди еще две, чтоб мнимая прямая, между ними, была перпендикулярна первой. Перемножив длины прямых получишь свою площадь. А так как знаешь координаты своих точек, то сможешь посчитать координаты угловых точек площади, чтоб правильно нарисовать свои линии. Либо не считать, а рисовать линии через найденные точки, чтоб центр линии проходил через точку, но тогда надо будет посчитать угол, под которым линия будет проходить через точку.

Comments

[ambisinister One]

Взять любую точку периметра и вращать, измеряя удаление - приближение точки за полный оборот.
Или?

[Alexandroppolus]

Перемножив длины прямых получишь свою площадь.

не уверен, что это будет площадь минимальной рамки. Например, для контура в виде квадрата 1х1 получим квадратную рамку площадью 2

[profesor08]

Alexandroppolus, еще меньше не сделать, тогда дальние точки вылезут за пределы.

[profesor08]

ambisinister One, нет, посчитать расстояния между точками, и из них выбирать.

[Александр Скуснов]

Alexandroppolus, 1х1 = 1

[Александр Скуснов]

Кстати, у рамки два минимума: площадь и периметр. И это могут быть разные рамки.

[Wataru]

profesor08, Ваше решение не верно для квадрата 1x1. Найденные 2 самые далекие точки - будут диагональю длины sqrt(2). Перпендикуляр - вторая диагональ. В итоге площадь у вас будет 2. Когда как можно пустить рамку вдоль самого квадрата, касаясть его везде - площадь будет 1.