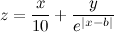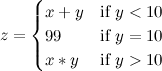Rsa97

На C++

#include <iostream>
#include <vector>
#include <set>
#include <time>

std::set<std::string> subSeqs;
struct _element {
    char digit;
    int  count;
};
std::vector<_element> elemSeq;

void recurse(std::vector<_element>::iterator elemRest, std::string subSeqHead) {
  bool fin = (elemRest+1 == elemSeq.end());
    for (int i = 0; i <= elemRest->count; i++, subSeqHead += elemRest->digit)
        if (fin)
            subSeqs.insert(subSeqHead);
        else
            recurse(elemRest+1, subSeqHead);
}

void main(void)
{
  int i;
  _element element;
  std::string initialSeq = "1234567890123";

    std::cout << "Initial sequence: " << initialSeq << "\n";

    clock_t start = clock();

    element.digit = initialSeq[0];
    element.count = 1;
    for (i = 1; i < initialSeq.length(); i++) {
        if (element.digit == initialSeq[i])
            element.count++;
        else {
            elemSeq.push_back(element);
            element.digit = initialSeq[i];
            element.count = 1;
        }
    }
    elemSeq.push_back(element);

    recurse(elemSeq.begin(), "");

    clock_t finish = clock();

    i = 0;
    std::cout << "Elements: (";
    for (std::vector<_element>::iterator t = elemSeq.begin();
                                                t != elemSeq.end(); t++) {
        if (i++ != 0)
            std::cout << ", ";
        std::cout << "{'" << t->digit << "', " << t->count << "}";
    }
    std::cout << ")\n";
    std::cout << subSeqs.size()-1 << " unique subsequences\n";
    std::cout << "Calculation time " << finish-start << " clicks, ";
    std::cout << ((float)(finish-start))/CLOCKS_PER_SEC << " sec\n";
/*     for (std::set<std::string>::iterator t = subSeqs.begin();
                                                t != subSeqs.end(); t++) {
        std::cout << *t << "\n";
    } */
}

Результаты:

Initial sequence: 8246
Elements: ({'8', 1}, {'2', 1}, {'4', 1}, {'6', 1})
15 unique subsequences
Calculation time 0 clicks, 0 sec
================================================================
Initial sequence: 88885
Elements: ({'8', 4}, {'5', 1})
9 unique subsequences
Calculation time 0 clicks, 0 sec
================================================================
Initial sequence: 12345678901234567890
Elements: ({'1', 1}, {'2', 1}, {'3', 1}, {'4', 1}, {'5', 1}, {'6', 1}, {'7', 1},
 {'8', 1}, {'9', 1}, {'0', 1}, {'1', 1}, {'2', 1}, {'3', 1}, {'4', 1}, {'5', 1},
 {'6', 1}, {'7', 1}, {'8', 1}, {'9', 1}, {'0', 1})
1043455 unique subsequences
Calculation time 4383 clicks, 4.383 sec
================================================================
Initial sequence: 11223344556677889900
Elements: ({'1', 2}, {'2', 2}, {'3', 2}, {'4', 2}, {'5', 2}, {'6', 2}, {'7', 2},
 {'8', 2}, {'9', 2}, {'0', 2})
59048 unique subsequences
Calculation time 187 clicks, 0.187 sec

Несколько сократить количество вариантов при переборе можно сгруппировав подряд идущие одинаковые цифры. Скажем для (1 1 1 2 1 1) получим исходный набор ((1, 3), (2, 1), (1, 2)). После этого рекурсивно его перебираем.

функция рекурсия(набор, результат) {
    если набор пуст {
        если результат уникален { 
            добавить результат в список уникальных
        }
    }
    ((цифра, количество), следующий_набор) = набор;
    для i от 0 до количество {
        рекурсия(следующий_набор, результат+(цифра i раз));
    }
}
рекурсия(исходный_набор, '');

Первый шаг рекурсии даст варианты '', '1', '11' или '111'. Второй шаг к каждому из них допишет '' или '2'. Третий шаг к каждому из 8 получившихся вариантов допишет '', '1' или '11'. То есть вместо 2⁶ = 64 вариантов для поиска уникальности получим 4*2*3 = 24.
Чем больше будет в исходной последовательности групп подряд идущих одинаковых цифр тем больше будет выигрыш. Если таких групп нет, то упрёмся в полный перебор.