Существует ли алгебра логики с оператором логического вычитания?

Griboks, на простой вопрос ответить не можете. На этом с вами всё

Существует ли алгебра логики с оператором логического вычитания?

Griboks, в вычитании по модулю возможно вычесть 7 из 8. А в XOR нет. Это вы понимаете?

Существует ли алгебра логики с оператором логического вычитания?

Griboks, В третий и последний раз спрашиваю, почему 7 это в вашей вселенной true, а 8 - false?

Существует ли алгебра логики с оператором логического вычитания?

Griboks, повторю ещё раз вопрос: почему 7 это true, а 8 - false?

Потому что мы работаем на mod 2, где существую только два числа: 0 и 1.

Некорректно говорите, РЕЗУЛЬТАТ вычисления по модулю два это ЧИСЛА 0 и 1.
Может ли в качестве аргумента XOR выступать ЧИСЛО?

Ответьте на всё вопросы, пожалуйста, гуру логики.

Существует ли алгебра логики с оператором логического вычитания?

Griboks, хотел бы я сказать, что таких тугих как вы не видела но есть и похуже. Повторю вопрос, почему 7 это true, а 8 это false? Вы почему выдаёте желаемое за действительное? У меня отлично получилось с 7 - 8, а вы почему то не видите. Может вы специально нервируете? Я могу прорешать хоть миллион примеров с натуральными числами, только какой в этом смысл, если натуральное число и true false это разные вещи? Как вам вдолдонить в голову, что это сложение?

Существует ли алгебра логики с оператором логического вычитания?

Griboks,

Ничего не понял, опять формул нет. Какие-то вероятности... Ну давайте, вычислите true & false | true с вероятностью 1/16, интересно на это посмотреть.

Я уже не удивляюсь, что вы ничего не понимаете. Скорее всего, вы это не изучали в учебных заведениях, но вот специально для вас отрывок из лекций (за почерк извините).

Можете увидеть 16 возможных состояний таблицы истинности из двух аргументов. Формулу вероятности вы не знаете? Вероятность = количество желаемых исходов деленное на общее количество исходов.В данном случае равна 1/16.

По поводу количества аргументов вот вам из излюбленной википедии (крайне советую ей не пользоваться, очень в ней много косяков) из уже упомянутых статей, которые вы видимо не дочитали, так как искали только то, что подтверждает вашу "идею", а то что опровергает пропускали, как всегда.

Ну давайте проверим вместе: (7 mod 2) - (8 mod 2) = 1 - 0 = 1, когда true ⊕ false = 1. Убедились? Всё работает как часы.

А должно работать как оператор!
В чем я здесь должен убедиться? Где в таблице истинности 7 и 8 в аргументах? Почему у вас 7 это истина, а 8 ложь? Совсем для маленьких объясняю: Невозможно произвести операцию XOR над числами 7 и 8, так как XOR - это оператор булевый, который может работать только с парой ИСТИНА-ЛОЖЬ. А вы упорно делаете в рамках своей "идеи" их тождественными, и, что хуже всего, считаете, что это доказывает, что логическое вычитание это XOR.

Подумайте, пожалуйста, еще вот над чем: сложение и вычитание по модулю 2 имеют один и тот же результат, но сложение по модулю 3 и более и соответствующее вычитание имеют разные результаты. Если результат двух операций одинаковый для модуля два, можно ли говорить, что сложение и вычитанию по модулю - тождественные операции?
Отвечу за вас - нельзя. Назовите XOR тождественным со сложением по модулю 2 как все нормальные знающие люди и один вопрос сразу отпадет.

И определения демагогии и софистики сюда пришлите, чтобы я убедился, что вы их хотя бы прочитали и понимаете, в чем бездумно обвиняете.

И давайте уже определимся, с чем именно вы не согласны. Изначально ваш косяк был в том, что вы не написали про "по модулю 2" и отождествили арифметическую операцию "вычитание по модулю" и логическую булеву "исключающее или". Я вам говорю, не вычитание, а сложение, с ним отождествлять можно и нужно. Отсюда последовало следующее, что вы по ошибке из википедии так же назвали XOR логическим вычитанием, хотя это по факту взаимная разность, что вы в следующем же предложении и вставили.
В булевой алгебре под понятием "логическое вычитание" может использоваться только одна операция, она в скинутых ранее таблицах третья в первой строке и называется декремент. два доказательства я кидал вам в самом начале, но вы их не видите. вот третье

Ну и с чем вы не согласны?

Существует ли алгебра логики с оператором логического вычитания?

Griboks,

Для ассоциативной операции результат вычисления x1, x2,..., xn не зависит от порядка вычисления (расстановки скобок)

- википедия почти сразу после определения. Черника форте помогает зрению.

Сравнить бинарный оператор с функцией от двух аргументов - в этом главная претензия, если вы не поняли. Оператор с функцией...

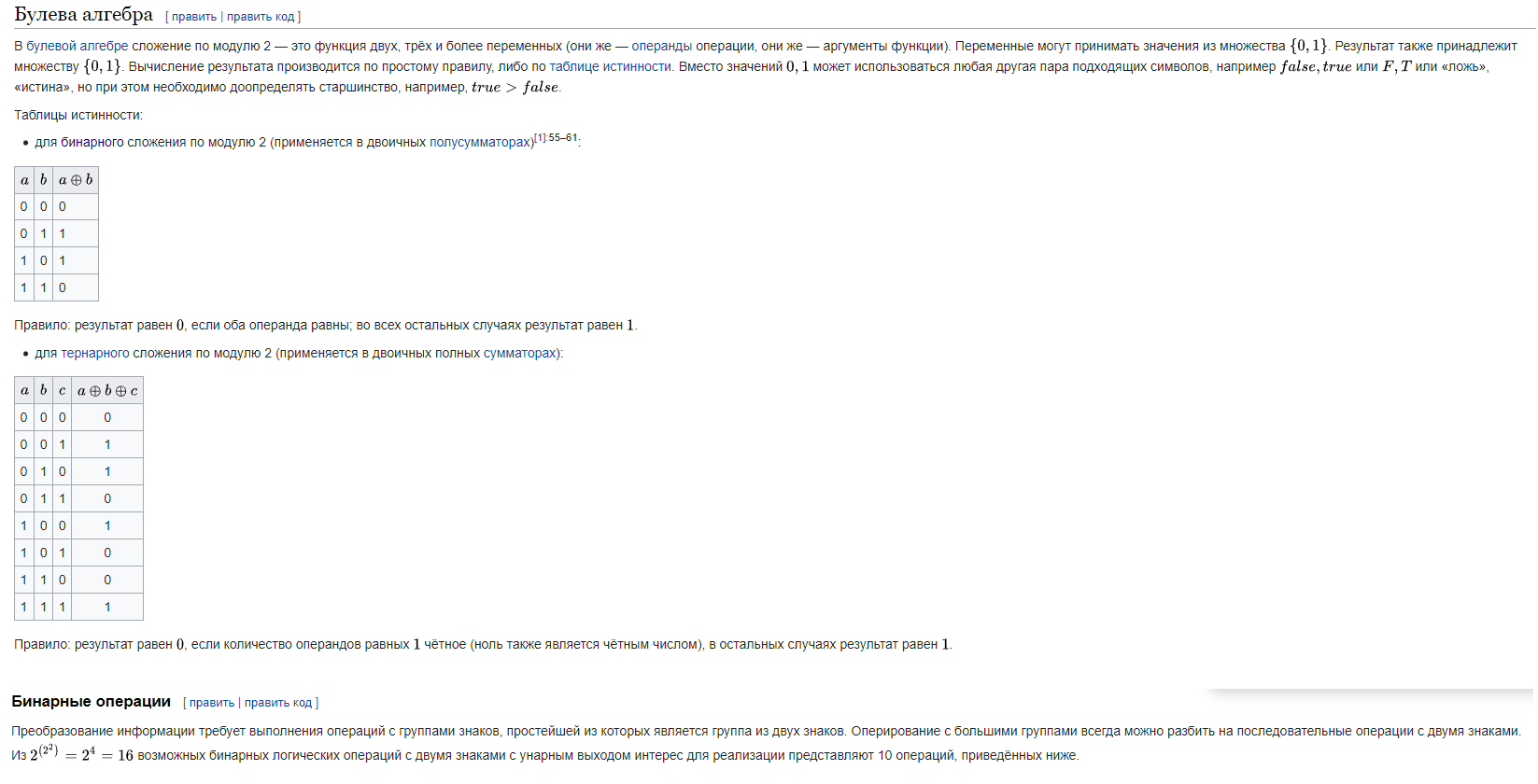
Составим таблицу истинности для математического вычитания.
A B A-B
0 0 0
0 1 1
1 0 1
1 1 0

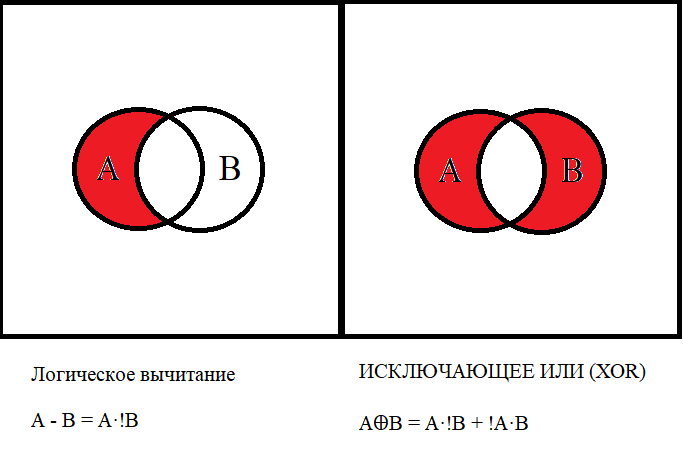
Получаем, что A-B=A xor B, следовательно - := XOR.

Здесь вы сравниваете математическое вычитание (даже не упомянув что оно по модулю 2) с логической операцией исключающее или.

Вовсе да, уловка ещё какая. Неужели так сложно увидеть всё доказательства, что я написал?
Давайте вам доказательство из теории вероятностей дам, раз остальные не устраивают, с формулой. Таблица истинности для двух аргументов может принимать 16 состояний в бинарной логике. Вероятность того, что вы, применив любые математические вычисления с бинарным или двоичным результатом, получите ту же таблицу истинности, Р=1/16. Если таблица истинности для вычитания по модулю 2 совпала с таблицей истинности для сложения по модулю 2, это не является доказательством эквивалентности двух операций. Вы же утвержаете, что сложение и вычитание это эквивалентные операции, только исходя из одинакового результата.

Теперь снова прочтите цитаты из той же википедии, что XOR это СЛОЖЕНИЕ по модулю 2, ВЗАИМНАЯ разность множеств и перестаньте называть это вычитанием.

А если в качестве массивов я буду использовать числа А = 7, В = 8, то результат не будет совпадать с таблицей истинности XOR. Почему же, если жто эквивалентные операции? Ответ: потому что XOR это логическая операция, а вычитание по модулю - математическая.

На всё ответил? Удовлетворил? Теперь ваша очередь отвечать на вопросы.

Существует ли алгебра логики с оператором логического вычитания?

Griboks, доказательств было предостаточно, книжки, не поверите, читал по теме достаточно много ввиду образования и рода профессиональной деятельности.
Это хорошо, что вы знаете слова "Демагогия" ,и "Софистика". Жалко, что не знаете значения этих слов.

Попробуйте дочитать статью излюбленной вами Википедии дальше и увидите, что аргументы у бинарных операторов не ограничены двумя, они складываются из простейших операций с двумя аргументами.

И никакой связи булевой алгебры с двоичным арифметикой, никакого отождествления логического и арифметического вычитания не подрузамевается.

Сейчас вы использовали софистскую логическую уловку, пропустив мимо все аргументы, доказывающие на 100% вашу правоту и сместив фокус на более отстраненное. Как обещал, обозначил.

Дальше ни вижу смысла спорить, пока не ответите на каждый аргумент достойным контраргументом, а то зубы уже от вашей упрямости скрипят.

Существует ли алгебра логики с оператором логического вычитания?

Griboks, до сих пор называете XOR вычитанием по модулю 2... Вы неисправимы.

Ах если бы автор сам пришёл и объяснил вам суть своего вопроса, было бы проще. В упор не видеть замену отрицания на логическое вычитание в вопросе и интерпретировать это по-своему... Я умываю руки.

Вы наверное ещё не знаете отличие булевой системы исчисления от двоичной, это тяжело.

Это бинарный оператор или функция от двух аргументов. Никакого третьего аргумента у неё нет.

Просто нет слов. Берите учебники, ищите определения. "Бинарный оператор или функция от двух аргументов..." На этом у меня к вам больше нет вопросов, тут просто нет никакой базы в вашей голове. Просто гуглите, пожалуйста, операторы 3-И, 3XOR, 4-ИЛИ-НЕ и скажите АСЕМ, что этих операторв не бинарные, потому что у них больше двух аргументов.

Существует ли алгебра логики с оператором логического вычитания?

Griboks, хорошо, попробую разжевать для самых непонятливых.

Тезис: Модуль арифметической разности А и В эквивалентен операции |A-B| <=> XOR.

Доказательство:
Сравним таблицы истинности
А В |A-B|
0 0 0
0 1 1
1 0 1
1 1 0

XOR:
А В AꚚB
0 0 0
0 1 1
1 0 1
1 1 0

Вывод: модуль разности эквивалентен XOR.

Не похоже на бред? Вот вы тоже самое тут пишете. Если РЕЗУЛЬТАТЫ двух РАЗЛИЧНЫХ операций при одном и том же наборе входных данных ОДИНАКОВЫЙ, это не значит, что РАЗЛИЧНЫЕ операции стали одной и той же операцией. Можно собрать любую нейронную сеть, или длиннющую логическую схему, где из двух входов А и В получится та же таблица истинности. Я уже молчу о том, что вычитание по модулю происходит в двоичной системе исчисления, а не в булевой бинарной.

Момент №2. Если XOR это вычитание по модулю два, то как быть при наличии трёх и более входов? вы будете искать (A-B) mod 2 - C mod 2? Или может (A-B-C)mod2? Или (B-C-A)mod2? Кто определяет, что будет уменьшаемым, что будет вычитаемым в этой разности? Может люди неглупее вашего будут и не зря назвали это СЛОЖЕНИЕМ по модулю 2? Хотя это чистая формальность и опять таки отождествление арифметической операции с логической.

Момент №3. Вас спросили, есть ли логическое вычитание, вы сказали, XOR это вычитание по модулю 2. Это все равно что:
- Какой краской лучше покрасить забор?
- Краска горит тем же цветом, что и дерево.
К чему это?

У вас отсутствует логика в теме про алгебру-логики. Это греховно.
И да, вы использовали столько софистких приемов за этот спор против ни одного использованных мной. Вы хоть знаете, что такое софистика? Если вы продолжите отстаивать свою точку зрения я так и быть, покажу вам, какие логические уловки вы используете чтобы не остаться проигравшим в явно проигранном споре. Будет полезно знать и определять, кто софист, а кто нет.

Существует ли алгебра логики с оператором логического вычитания?

Griboks, Можете, пожалуйста, повторить ваше "строгое математическое доказательство"? Я что-то не наблюдаю его.
А дальше вы описываете мои ответы будто под инверсией: рассуждения не абстрактные, а конкретные; ничего не доказал? Разными способами доказал, расписал так, что даже ежик поймёт, даже картиночки вставил. Не опроверг? Аналогичным образом опроверг ваше утверждение, что логическое вычитание это XOR (написать таблицу истинности для XOR и сказать, что это таблица истинности для логического вычитания это гениальное доказательство). Я даже книгу указал, учебный материал, где чётко различено логическое вычитание и XOR, но видимо всё выше перечисленное вас не переубедит, потому что вы не хотите быть переубежденным. Это кстати не ваша вина, сейчас много людей поддались этому недостатку, триумф мнения в головах, а на знания всё закрывают глаза.
Кстати вашу ссылку (вами предоставлена только одна на Википедию) изучил от и до, так что и тут ошиблись.

Ничего страшного в этом нет, но тут я думаю что больше сказать нечего, и в основной массе рациональных людей меня поймут. А с вами просто так спорить не вижу смысла, разве что если не предоставите контраргументы к моим аргументам и не приведете свои тезис-доказательство-вывод.
Без обид и агрессии, человек человеку не рознь)

Существует ли алгебра логики с оператором логического вычитания?

Griboks, Википедия - не панацея, там много чего могут написать, но если для вас она авторитет, то автор вопроса прислал статью, где нерусским по белому написано:
As 1 and 0 are the only permissible numbers in Boolean algebra, there can be no negative numbers.
"This means that there is no subtraction, as 0-1 is the same as 0+(-1). -1 is not an allowed number, so the concept of subtraction is meaningless in Boolean algebra.
As division is just a variation on subtraction, just as multiplication is a variation on addition, division is also meaningless in Boolean algebra."
что переводится как:
"Поскольку 1 и 0 являются единственно допустимыми числами в булевой алгебре, отрицательных чисел быть не может.
Это означает, что вычитания нет, поскольку 0-1 совпадает с 0+ (-1). -1 - недопустимое число, поэтому концепция вычитания не имеет смысла в булевой алгебре.
Поскольку деление - это всего лишь разновидность вычитания, точно так же, как умножение - это разновидность сложения, деление также не имеет смысла в булевой алгебре.".
Недолго поискав в интернете можно понять, что логическим вычитанием XOR обзывают очень очень редко, и в книжках для логического вычитание есть свой символ /, который далее и означает конъюнкцию первого слагаемого с отрицанием второго (*!, И НЕ). Например, в книге Матлогики Лагодинского:

Из одного или нескольких высказываний можно получить другое высказывание, используя логические связки: (конъюнкция, логическое умножение, и), (дизъюнкция, логическое сложение, неисключающее или), ¬ (отрицание, не), → (импликация), ↓(стрелка Пирса), | (штрих Шеффера), (символ Жегалкина, исключающее или, сложение по модулю 2), ~ (эквиваленция), \ (логическое вычитание) и это высказывание называется логической функцией исходных высказываний.

На что я отвечаю, что это xor

В вопросе XOR было упомянуто лишь потому, что выражение НЕ (A И B) И (A ИЛИ B) и есть одна из форм записи XOR. Связь между "вычитанием" и "XOR" в вопросе отсутствует. Единственное, где можно назвать XOR разностью - это ВЗАИМНАЯ разность двух множеств, где разность А и В объединяется с разностью В и А.

Меня не интересует спор ради спора, главное чтобы ваши ложные выводы

Получаем, что A-B=A xor B, следовательно - := XOR.

не обманывали товарищей.

Существует ли алгебра логики с оператором логического вычитания?

Griboks,

Это обычное кольцо по модулю 2. Поэтому все простейшие операции естественным образом работают, в том числе и вычитание. -1 mod 2 = 1

XOR - это сложение по модулю 2, вычитание тут вообще не причем. Причем здесь теория множеств и вычеты, как они относятся к булевой алгебре - не понятно.

Если вы говорите конкретно про алгебру логики, то в ней и 0, 1 тоже отсутствуют - есть только ложь, истина, клнъюнкция, дизъюнкция и отрицание.

Речь всей темы идет конкретно про алгебру-логику им ничто больше. Очевидно, что 1 - истина, 0 - ложь, "+" - дизъюнкция, "*" - конъюнкция, "!"- отрицание. Для удобства записи используют эти символы, но при этом используются свои законы Алгебры-логики, сложения, вычитания, деления, умножения здесь нет.

Хотелось бы увидеть ваше доказательство.

Доказательство 1 (графическое). Интуитивно диаграммы множеств отражают законы булевой алгебры:

Доказательство 2 (гугло-онлайн-калькуляторное). Воспользовавшись любым онлайн калькулятором,

и получаем таблицу истинности и знакомое выражение A*⌐B

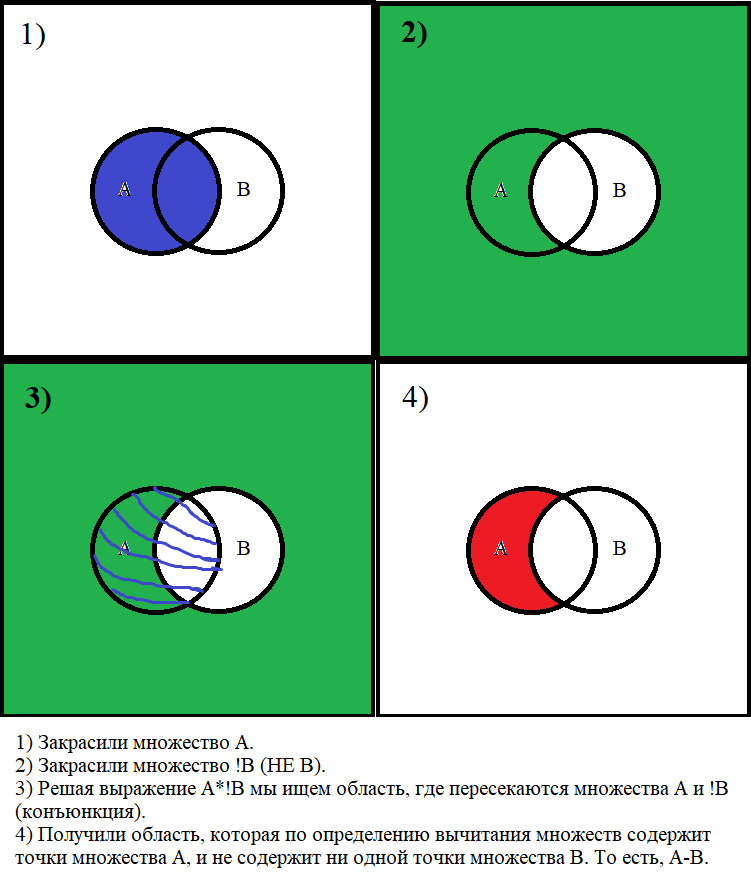
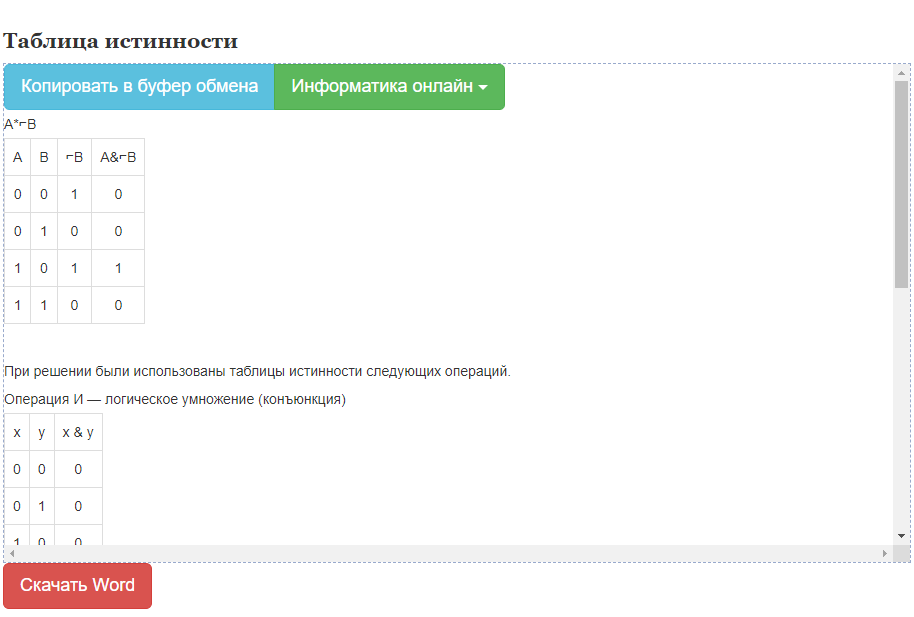
Вот я выше привёл таблицу интстинности вычитания по модулю 2, таблицу xor, они совпали, ч.т.д.

Я не слышал про "Таблицу истинности вычитания по модулю 2", не могу ничего про нее сказать. А здесь вижу таблицу истинности XOR, которое еще называют СЛОЖЕНИЕМ ПО МОДУЛЮ 2. Да, есть такое назваоние у оператора XOR. Но это не вычитание. Даже если проводить аналогию с множествами, то разность двух множеств и XOR имеют разные диаграммы, что приводил в предыдущем ответе.

И почему бы тогда не использовать симметричную разность множеств?

Симметричная разность множеств наиболее похоже определяет XOR, потому что это разность А-В объединенная с разностью В-А.

Итого, если отвечать на исходный вопрос автора, есть ли вычитание в алгебре-логике, ответ - нет. Представлять отрицание !А = 1- А только усложняет работы с логическими выражениями, потому что арифметическая разность и разность множеств сильно отличаются, имеют свои свойства и запреты, изучать которые можно, но в рамках булевой алгебры это будет ненужное усложнение.
Вы ответили ему на этот вопрос (осмелюсь перефразировать) "Да, вычитание есть, и это XOR". И вот человек три года как думает, что:
а) записывать отрицание как 1-А можно в булевой алгебре так же, как в теории множеств;
б) это эквивалентно ИСКЛЮЧАЮЩЕМУ ИЛИ.

Больше логики в этот мир и всего доброго.

Существует ли алгебра логики с оператором логического вычитания?

Griboks, Dmitry221060, рано закрыли вопрос. В булевой алгебре НЕТ вычитания и деления, поскольку это предполагало бы ответы для выражения 0-1=-1, а такого в бинарной системе быть не может.
Изначально в данной алгебре есть 3 операции, и другие лишь являются лишь следствием из них.

Аналогом вычитания в булевой алгебре могло бы служить выражение В - А = В · Ᾱ, но это только аналог. Кстати, сложение и умножение тоже аналоги? значок "+" не означает того сложения, которое мы знаем.
Нельзя написать А+А=2А. Что такое 2? Две истины? Двойная истина? Это жесткая логика, Аристотель еще давным давно сформулировал закон исключения третьего.

Dmitry221060, по поводу примера в основном вопросе - использовали сложный и ложный путь, но пришли к верной таблице истинности ввиду схожести законов булевой алгебры и простых математических. Закон де Моргана и сочетательный закон без прибегания к "вычитанию" и "двойной истине" в три действия решает данный пример:
!(A·B)·(A + B) = (!А + !В)·(A + B) = !А·А + А·!В + !А·В + В·!В = (первое и четвертое слагаемое по закону исключения третьего - ложь (нуль)) = А·!В + !А·В.
Получилось выражение операции ИСКЛЮЧАЮЩЕЕ ИЛИ (АꚚВ).

Теперь по поводу этого исключающего или (XOR).
Griboks, тут уж вы совсем не правы. Учитывая, что А - В в булевой алгебре означать может только А·!В, то таблица истинности должна быть следующая:
A B A-B
0 0 0
0 1 0
1 0 1
1 1 0
Если записать XOR через знак "-" то получится выражение (А-В)+(В-А). Была бы это просто алгебра, мы бы не побрезговали и раскрыли бы скобки и получили бы нуль. Что уже ошибочно. Приложу картинку с кружочками для понимания различия XOR и "логического вычитания".

Поэтому, заклинаю всех, при работе над логическими выражениями используйте законы алгебры логики и не отходите от операций И, ИЛИ, НЕ, и будет всем хорошо мир дружба жвачка.