Как нарисовать квадрат & треугольник?

Question

[JTester]

Здравствуйте! Как нарисовать квадрат и треугольник? Использовать canvas не нужно.
Нужно на тригонометрических функций

Желательно описать каждую строчку, чтобы я хоть что-то понял. Заранее спасибо

Comments

[Froggyweb]

А рисовать его где? можно svg можно css

Нужно на тригонометрических функций

svg вполне подходит

[JTester]

Froggyweb, не нужно мне svg, нужно нарисовать через тригонометрические функции и без использования canvas.

[hellcaster]

JTester, а где нужно нарисовать?

[JTester]

hellcaster, смысле где?

[Froggyweb]

JTester, ы прямом. описать как рисуется треугольник в вакууме или на конкретной технологии
svg - 'это совсем не конвас

https://www.math10.com/ru/geometria/formuli-trigon... :)

[Василий Банников]

JTester, ну типа в JS можно рисовать только при помощи канваса и SVG.

Answer 1

[Александр]

Это, наверное, лучший вопрос. Итак, краткий экскурс. Для того, чтобы нарисовать фигуру нам понадобятся всего две математические функции: sin и cos. А ещё будет неплохо вспомнить, какие числа в какой четверти круга они возвращают:

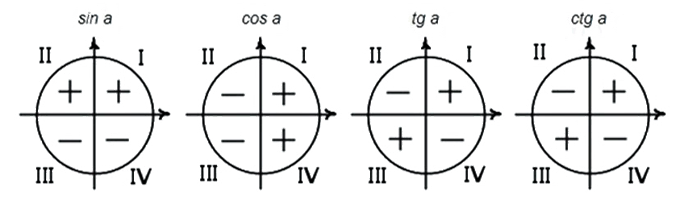
Следовательно, sin(x) вернёт числа больше или равные нулю в четверти 1 и 2 (от 0° до 180°); cos(x) вернёт числа больше или равные нулю в четверти 3 и 1 (от 270° до 90°). Итак, для того чтобы нарисовать квадрат, необходимо всего 4 точки, а для треугольника - 3 (внезапно). Для квадрата нам надо разделить 360° на 4 равные части (то бишь по 90°).

Однако, если у вопроса тэг JavaScript, я подозреваю, что надо бы действовать по-другому. Для начала вспомнить, чем радианы отличаются от градусов, дам подсказку - 1 радиан равен числу Пи, и одновременно равен 180°. Следовательно, делить мы будем уже не градусы, а радианы (потому что в JavaScript'е математические функции синуса и косинуса работают именно с ними). Поделив нужное количество радиан на 4 части, мы получим шаг угла квадрата. Значит циклом в 4-е шага можно получить все координаты, однако - всё не так просто.

Надо ещё вспомнить, что синус и косинус возвращают числа от [-1; 1], а это значит, что квадрат будет очень маленьким, если мы впишем его в окружность, радиусом 1. Для решения уже этой проблемы, умножим полученное значение синуса и косинуса на радиус, к примеру на 100.

Теперь при помощи цикла (сколько точек у фигуры, столько и итераций) мы можем получить все точки для координаты x (косинус) и для координаты y (синус), после чего последовательно соединить, получив квадрат.

Если мы хотим повернуть квадрат, к примеру на 45°, то снова превращаем градусы в радианы и прибавляем к радианам в синусе и косинусе в тот момент, когда высчитываем координаты точек.

Ну а для треугольника (и вообще любой фигуры, которую можно вписать в окружность) алгоритм действий отличается только количеством итераций.

Comments

[JTester]

Все равно не понял :(

[Александр]

JTester,

Да ладно

Окей. Возьмем стартовый угол 0°. Для квадрата будут следующие координаты:
X₁ = cos(0° * Радиан + Стартовый_Угол * Радиан) * Радиус = 100.00
Y₁ = sin(0° * Радиан + Стартовый_Угол * Радиан) * Радиус = 0.00
X₂ = cos(90° * Радиан + Стартовый_Угол * Радиан) * Радиус = 0.00
Y₂ = sin(90° * Радиан + Стартовый_Угол * Радиан) * Радиус = 100.00
X₃ = cos(180° * Радиан + Стартовый_Угол * Радиан) * Радиус = -100.00
Y₃ = sin(180° * Радиан + Стартовый_Угол * Радиан) * Радиус = 0.00
X₄ = cos(270° * Радиан + Стартовый_Угол * Радиан) * Радиус = -0.00
Y₄ = sin(270° * Радиан + Стартовый_Угол * Радиан) * Радиус = -100.00
при:
Радиан = π / 180
Стартовый_Угол = 0°
Радиус = 100

Другие начальные данные

X₁ = cos(0° * Радиан + Стартовый_Угол * Радиан) * Радиус = 56.29
Y₁ = sin(0° * Радиан + Стартовый_Угол * Радиан) * Радиус = -32.50
X₂ = cos(90° * Радиан + Стартовый_Угол * Радиан) * Радиус = 32.50
Y₂ = sin(90° * Радиан + Стартовый_Угол * Радиан) * Радиус = 56.29
X₃ = cos(180° * Радиан + Стартовый_Угол * Радиан) * Радиус = -56.29
Y₃ = sin(180° * Радиан + Стартовый_Угол * Радиан) * Радиус = 32.50
X₄ = cos(270° * Радиан + Стартовый_Угол * Радиан) * Радиус = -32.50
Y₄ = sin(270° * Радиан + Стартовый_Угол * Радиан) * Радиус = -56.29
при:
Радиан = π / 180
Стартовый_Угол = -30°
Радиус = 65

JS

const startAngle = 0;
const points = 4;
const radius = 100;
const radian = Math.PI / 180;

for (let index = 0; index < points; index++) {
  const angle = (360 / points * index) * radian + startAngle * radian;
  const x = Math.cos(angle) * radius;
  const y = Math.sin(angle) * radius;
  
  console.log(`X(${index + 1}) = ${x.toFixed(2)}`);
  console.log(`Y(${index + 1}) = ${y.toFixed(2)}`);
}

Советую подтянуть математику, и хоть немного геометрию за 5-8 классы.