Как вывести определенное значение в центр массива при его разной размерности?

Question

[Александр Фандеев]

Всем привет. Столкнулся с небольшой проблемой при решении задачи.

Необходимо, в точности как на изображении, создать прямоугольник из символов '#' и центр этого прямоугольника заполнить пустыми символами. Проблема нарастает тогда, когда размерность массива растет. В задаче требуется, чтобы его размерность могла быть от 3 до 100.

Comments

[Сергей Соколов]

там только один хэш в центре, или чтобы через-один они были, в клеточку?

[Александр Фандеев]

Сергей Соколов, в размерности 3x3 один пустой символ, по центру. В 4x4, - 4 пустых символа. В 5x5 только один по центру.

[Сергей Соколов]

Александр Фандеев, это я вижу. А в размерности 7x7 и 8x8?

[Александр Фандеев]

Непонятно. Дали знакомому задачу, но в условиях ничего не написали относительно других размерностей. Я решил для трех предыдущих, а насчет остальных не знаю, что сделать. По этому и решил здесь спросить.

[Wataru]

Александр Фандеев, Нужен полный текст задачи. По одному только скриншоту примера входных и выходных данных ничего не понятно. Может надо через один символ # внутри ставить, если есть место. А может, надо полный квадрат размера N-4 на N-4 заполнить, оставив узкий коридор между ним и внешним квадратом. А может надо N/2 вложенных квадратов нарисовать. А может N=5 единственный особый случай.

[Александр Фандеев]

Wataru, привёл его Вам чуть-чуть ниже. Не знаю, когда я прочитал его, то не раскрыл для себя завес. По этому и скидывал скриншот.

[Wataru]

Александр Фандеев, Отредактируйте вопрос, чтобы там была вся задача целиком.

Answer 1

[Wataru]

Edit:

Раз задача построить концентрические вложенные квадраты, то есть 2 подхода.

Простой для понимания, но менее эффективный (но все-равно отлично быстрый для смешных ограничений в задаче) - напишите функцию, которая в двумерном массиве рисует квадрат заданного размера вокруг центра. Это тупо 4 последовательных, не вложенных цикла. Каждый рисует одну сторону квадрата. Тупо цикл до n, где n - длина стороны квадрата. Там одна координата фиксирована, а другая пробегает вдоль стороны. Надо чуть-чуть подумать, и составить формулы, какие строки и столбцы будут закрашены.

Заведите двумерный массив, заполните его пробелами, и потом циклом от n%2 до n с шагом 2 рисуйте квадраты.

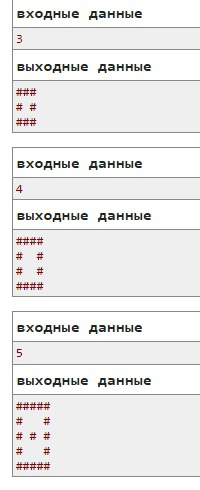
Второй, более эффективный, подход - это немного подумать. Возьмите клетчатый лист, или в редакторе каком-либо нарисуйте ответ для n=9,10. Подумайте над паттернами. Первая строка будет всегда из n #. Вторая будет #, n-2 " ", #. Следующая "# #...# #" и так далее.

Одни строки будут иметь в середине отрезок из "#" какой-то длины, а по краям заданное количество чередующихся "#" и " ". Соседние строки будут содержать в середине отрезок из пробелов, а вокруг чередующиеся решетки и пробелы. По номеру строки можно весьма просто вычислить длины среднего отрезка и чередующихся кусков. Соответственно можно вывести ответ сразу же не формируя его в массиве. Выводите чередующиеся "# " нужное количество раз. Потом выводите "#" или " " нужное количество раз. Потом выводите " #" нужное количество раз. Это один внешний цикл, несколько тупых формул, три вложенных последовательных цикла с выводом.

Подсказка для формулы - имеет значение, как близко строка к середине массива и четность n. Расстояние до середины можно получить как abs(n/2 - i)

Comments

[Александр Фандеев]

В создании этого цикла. Я не совсем понимаю, как его реализовать.

[Wataru]

Александр Фандеев, Сначала приведите полное условие задачи.

[Александр Фандеев]

[Wataru]

Александр Фандеев, Отредактировал ответ.

Answer 2

[longclaps]

Хрен знает, завезли ли вам слайсы, а у нас в питоне они всегда были:

def f(n):
    l = [' '] * (n * (n + 1) - 1)
    l[n::n + 1] = '\n' * (n - 1)
    l[:n] = l[-n:] = l[::n + 1] = l[n - 1::n + 1] = '#' * n
    print(''.join(l))

f(5)

ps а пятнышко в середине последнего квадрата не нужно?
pps слайсы - те же циклы

UPDATE концентрические квадраты

def f(n):
    l = [[' '] * n for _ in range(n)]  # двумерный массив
    for shift in range(0, n // 2 + 1, 2):
        # рисуем как умеем верхние стороны квадратов
        l[shift][shift:n - shift] = '#' * (n - shift * 2)
    for i, row in enumerate(l):
        for j, ch in enumerate(row):
            if ch == '#':
                # заполняем симметричные точки
                l[j][i] = l[j][n - i - 1] = l[n - i - 1][n - j - 1] = '#'
    for row in l:
        print(''.join(row))

f(17)

Comments

[Александр Фандеев]

ну, в середине последнего квадрата есть #.

[longclaps]

Александр Фандеев, а, я-то думал, что мне показалсь ) Так оно нужно?

[Александр Фандеев]

longclaps, да

[longclaps]

да

Информативно.
Александр Фандеев, если внутри квадарата со стороной 5 есть пятно размером 1х1 - что должно быть внутри квадрата 6х6? А 10х10? По идее, это должно быть в условии, которое ты, наверное, читал.
Ну так что там написано?

[Александр Фандеев]

longclaps, ничего. Даже «да» не написано. Вот условие

[longclaps]

Александр Фандеев, концентрические квадраты там написано.