Как найти ВСЕ кратчайшие пути между двумя вершинами?

Question

[empty_project]

Как можно в неориентированном графе найти все кратчайшие пути между двумя вершинами? Проблема вот в чем: может быть ситуация, когда из некоторой вершины u до вершины v есть несколько кратчайших путей и все они одинаковой длины. Что делать в такой ситуации? Вот пример такого графа:
Здесь из вершины 1 до вершины 3 три кратчайших пути одинаковой длины: 1-3, 1-4-5-3, 1-5-3

Answer 1

[longclaps]

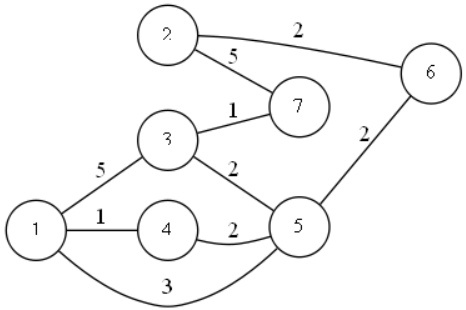
А зачем?
Представь себе шахматную доску, твои вершины - клетки, рёбра - границы смежных клеток и только они, переход шаг_влево/шаг_вправо/шаг_вверх/шаг_вниз.
Сколько существует кратчайших путей с левой нижней клетки в правую верхнюю? спойлер: 3432
А если вообразить аналогичный трёхмерный куб? 399072960
Вывод: задача хреново поставлена.
UPDATE
Для наглядности, пусть из одной из нужных вершин выходят 3 грани.
Строишь кратчайший путь, он проходит через первую из 3 граней. Путь запоминаешь, грань перерезаешь.
Строишь кратчайший путь, он проходит через вторую грань. Если он равновелик первому - запоминаешь, вторую грань перерезаешь, если больше - вторую и третью грани можешь совсем выкинуть.
Достаёшь первый путь, восстанавливаешь первую грань, идёшь по пути дальше до вершины с развилкой. режешь грань кратчайшего пути - ну, понятно, рекурсия.
На вырожденном графе, как я и обещал, хана.

Comments

[empty_project]

Я все это понимаю, однако препод дал это на защиту курсовой, что я могу поделать?

[empty_project]

У меня была идея как-то сюда поиск в глубину запихнуть, но дальше идеи не продвинулся

[longclaps]

empty_project, смотри апдейт.

Answer 2

[crazywu]

Мне кажется, что удобнее всего использовать обход в ширину. Записывая вес и путь до каждой встретившейся вершины.
В конечной точке соберутся все варианты.
Только эта штука будет жутко кушать память и не помешало бы сделать некоторые оптимизации:
-удалять/не записывать более длинные пути
-обьединять при дальнейшем поиске пути "слившиеся" в одной вершине
(Это то, что сразу приходит на ум, может есть ещё какие-то варианты)

Answer 3

[Zanak]

первая же ссылка у гугла
Не оно?