Проективное преобразование (поиск относительного положения точки)

Question

[andreyk6]

Добрый день.

Я сейчас пытаюсь разобраться с этой задачей:

Даны: правильный четырехугольник и квадрат, которые заданы своими координатами A(x1,y1), B(x2,y2), C(x3,y3), D(x4,y4) и M(0,0), N(1,0), P(1,1), K(0,1) соответственно.
Есть точка P(x,y), которая находится в этом четырехугольнике.
Нужно: Построить матрицу проективного преобразования для преобразования ABCD в квадрат MNPK. Далее нужно найти положение точки P`(x`,y`) в квадрате.

С построением матрицы я разобрался (скорее всего, я делаю это правильно):
Я вывел формулы для поиска матрицы преобразования из квадрата в четырехугольник:

.
.
.

.
.
.

.
.
.

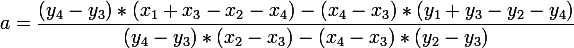
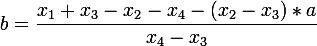
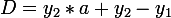
Получаю матрицу: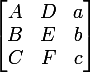



После этого, спасибо Хабраюзеру @Mrrl, я нахожу обратную матрицу (методом Гаусса).


Далее, я пытаюсь получать координаты точки в квадрате имея координаты точки в четырехугольнике:
.


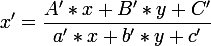
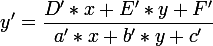
Но, получаю не верный ответ. Я подставляю совершенно разные точки, но получаю x и y 0,5.
Уверен точно, что алгоритм нахождения обратной матрицы работает правильно (Сверял результаты с онлайн сервисами).
В построении матрицы я тоже уверен, подставляя конкретный x1,y1,x2,y2,x3,y3,x4,y4 и решив систему получал одинаковые ответы на листике и в программе.

Где я ошибся? Что делаю не так?
Без свежего взгляда не обойтись.

Пример:
Дано:
A (CP[1]) {x=0 y=0 }
B (CP[2]) {x=1 y=0 }
C (CP[3]) {x=2 y=2 }
D (CP[4]) {x=0 y=1 }
Прямая матрица:
{0.66666666666666674, 0.00000000000000000, -0.33333333333333331}
{0.00000000000000000, 0.66666666666666663, -0.33333333333333337}
{0.00000000000000000, 0.00000000000000000, 1.0000000000000000}
Обратная матрица:
{1.4999999999999998, 0.00000000000000000, 0.49999999999999994}
{-0.00000000000000000, 1.5000000000000000, 0.50000000000000011}
{-0.00000000000000000, -0.00000000000000000, 1.0000000000000000}

Всем спасибо, все работало правильно.
Проблема была в обработке полученных данных.
Была опечатка при обращении к массиву, и брался Points[i+2] элемент, а нужно Points[i*2].
Мораль: Не нужно писать код ночью)

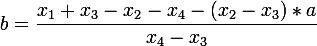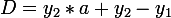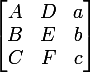
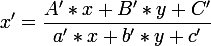Answer 1

[Mrrl]

А можете для какого-нибудь примера написать полученные прямую и обратную матрицы? Например, для A=M, B=N, D=K, C=(2,2) ?

Comments

[andreyk6]

Да, сейчас

[andreyk6]

@Mrrl, сделал
Дано:
A (CP[1]) {x=0 y=0 }
B (CP[2]) {x=1 y=0 }
C (CP[3]) {x=2 y=2 }
D (CP[4]) {x=0 y=1 }
Прямая матрица:
{0.66666666666666674, 0.00000000000000000, -0.33333333333333331}
{0.00000000000000000, 0.66666666666666663, -0.33333333333333337}
{0.00000000000000000, 0.00000000000000000, 1.0000000000000000}
Обратная матрица:
{1.4999999999999998, 0.00000000000000000, 0.49999999999999994}
{-0.00000000000000000, 1.5000000000000000, 0.50000000000000011}
{-0.00000000000000000, -0.00000000000000000, 1.0000000000000000}

[Mrrl]

Ошибок не видно, обе матрицы работают как надо. Меня, правда, смущает тип аргументов int в функции Convert, тем более, что вернуть 0.5 через int никак нельзя.

[andreyk6]

Да, тут я ошибся. Просто в самой программе такой функции нет, а тут я ее написал для того, чтобы было наглядно. Я просто упустил этот момент.

[andreyk6]

@Mrrl , еще пример и результат поиска относительных координат:
Дано:
A (CP[1]) {x=121 y=133 }
B (CP[2]) {x=565 y=133 }
C (CP[3]) {x=601 y=378 }
D (CP[4]) {x=89 y=373 }

Прямая матрица:
{433.98642822928309, -2.3571770716908702, -0.017723135877375059}
{-43.709404438767365, 190.92575443078397, -0.13156634200862208}
{121.00000000000000, 133.00000000000000, 1.0000000000000000}

Обратная матрица:
{0.0022928894434095996, -1.3990142942237635e-019, 4.0637191157347185e-005}
{0.00030571859245461333, 0.0047979101550530119, 0.00063666178054065854}
{-0.31810019544902507, -0.63812205062205063, 0.91040688305805340}

Результат после скармливания точки (200,200) в Convert():
Y = 0.30736229324029579
X = 0.19277926726329567

Результат после скармливания точки (100,200) в Convert():
Y = 0.30856120903964857
X = -0.026557356549236636

Результат после скармливания точки (250,250) в Convert():
Y = 0.51990279309487608
X = 0.30706872480030967

[Nashev]

А итоговый код вы нигде не публиковали? Мне б пригодился )

[Nashev]

И получается ли у вас тут в итоге коррекция перспективных искажений? Если одна сторона четырёхугольника узкая, сокращаются ли ближе к ней размеры по перпендикулярному к ней направлению?

Answer 2

[Nashev]

Мы для своего проекта Krutoscope искали решение проблемы коррекции перспективных искажений при вырезании изображения прямоугольного листа из фотографии этого листа. Везде реализации выпрямления четырёхугольника в прямоугольник попадались только через линейные пропорции! Прям везде, где искали!

И вот, благодаря этому Вашему вопросу, мы (Евгений Берёзкин, Никита Трубкин и я) таки написали на dart функцию, успешно выбирающую цвета точек для вырезанного листа из оригинальной фотки по координатам углов этого листа, и при этом, кажется, перспективные искажения успешно исправляющую!

import 'package:image/image.dart' as imglib;

class PerspectiveRectifier {
  late num a, b, c;
  late num a1, b1, c1;
  late num d, e, f;

  PerspectiveRectifier(imglib.Point topLeft, imglib.Point topRight,
      imglib.Point bottomLeft, imglib.Point bottomRight) {
    final x1 = topLeft.x;
    final y1 = topLeft.y;
    final x2 = topRight.x;
    final y2 = topRight.y;
    final x3 = bottomRight.x;
    final y3 = bottomRight.y;
    final x4 = bottomLeft.x;
    final y4 = bottomLeft.y;

    a = ((y4 - y3) * (x1 + x3 - x2 - x4) - (x4 - x3) * (y1 + y3 - y2 - y4)) /
        ((y4 - y3) * (x2 - x3) - (x4 - x3) * (y2 - y3));
    b = (x1 + x3 - x2 - x4 - (x2 - x3) * a) / (x4 - x3);
    c = 1;
    a1 = x2 * a + x2 - x1;
    b1 = x4 * b + x4 - x1;
    c1 = x1;
    d = y2 * a + y2 - y1;
    e = y4 * b + y4 - y1;
    f = y1;
  }

  Offset calculateSourceOffset(Offset relativeTargetOffset) {
    return Offset(
        (a1 * relativeTargetOffset.dx + b1 * relativeTargetOffset.dy + c1) /
            (a * relativeTargetOffset.dx + b * relativeTargetOffset.dy + c),
        (d * relativeTargetOffset.dx + e * relativeTargetOffset.dy + f) /
            (a * relativeTargetOffset.dx + b * relativeTargetOffset.dy + c));
  }
}

  imglib.Image copyRectifyWithPerspectiveCorrection(
      imglib.Image src, PerspectiveRectifier r, imglib.Image? toImage) {
    final dst = toImage ?? imglib.Image.from(src);

    for (int y = 0; y < dst.height; ++y) {
      for (int x = 0; x < dst.width; ++x) {
        final srsOffset =
            r.calculateSourceOffset(Offset(x / dst.width, y / dst.height));
        final srcPixel =
            src.isBoundsSafe(srsOffset.dx.toInt(), srsOffset.dy.toInt())
                ? src.getPixel(srsOffset.dx.toInt(), srsOffset.dy.toInt())
                : src.getColor(0, 0, 0);
        dst.setPixel(x, y, srcPixel);
      }
    }
    return dst;
  }

Собираюсь сделать PR в package:image