Как эффективно находить макс. значение постоянно растущей величины?

Question

[Сергей Соколов]

Целочисленная величина постоянно растёт в результате активности пользователей соц.сети. Есть API, через который только можно узнать, есть ли уже значение X или нет? Хочется узнавать в любой момент, какое значение сейчас самое большое из созданных, выполнив минимум запросов к API (предположим, запросы платные).

Некоторая история значений уже накопилась и можно попытаться построить модель – линейную или гиперболу. Но чем дольше не было новых измерений, тем больше возможный разброс от спрогнозированного.


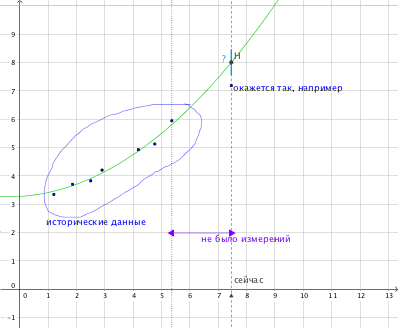
Совсем грубый вариант без модели – двоичный поиск в диапазоне от последнего найденного значения (нижняя граница) на некую большую величину (эмпирическую) вверх.

Вопрос: как правильно выполнять поиск методом научного тыка, если построить-таки модель, вписывающуюся в исторические данные, чтобы минизировать число тыков?

Т.е. из модели получается гипотеза, что на данный момент времени значение достигнет величины H. Можно её проверить: она либо есть, либо её ещё нет. На какой шаг теперь отступить от H, чтобы сделать следующую проверку?

Answer 1

[Limbend]

Какой то расплывчатый у вас вопрос получился, от чего сказанное мной возможно вам и так понятно.

Если есть некий сплайн по старым результатам, то почему бы не отталкиваясь от него, получить некое число N.
Далее проверить, достигнуто ли N+M и N-M.
Соответственно выяснив находится ли искомое значение в отрезке [N+M; N-M].

M - заранее рассчитать от степени разброса значений от сплайна и вашей требуемой точности.
Если M получится слишком большим и точность вас не устроит, то проделывать такое придется несколько раз.
Если M получится меньше разброса, то придется делать больше проверок (т.е. запросов)

Если удалось спрогнозировать только некий сплайн, без каких либо паттернов, то это единственный вариант.

При таком подходе вычислять точное число - все же затратно...

P.S. Не стоит проверять само число N (вы его назвали H) так как разброс все равно будет. Брать нужно достаточно широкий отрезок, проверять его края, и далее его резать по полам (Т.е. алгоритм логарифмического поиска).

Comments

[Сергей Соколов]

как выбрать оптимальное значение M? А если, к примеру, N-M, окажется, ещё нет, то следующую итерацию сделать на N - M - M, или, скажем, N - M * 1.5 ?

[Сергей Соколов]

точность требуется абсолютная – надо найти имено максимальное значение на сейчас, полагая, что обновления значения не происходят во время этого поиска.

[Limbend]

Сергей Соколов: В ваших интересах подобрать число M таким, чтоб оно при любом раскладе охватило истинную величину.
1 - кода в алгоритме будет меньше.
2 - проверок будет меньше.

[Limbend]

У вас уже есть некие результаты, попробуйте подогнать число M на них всех. Чтоб каждый результат был в рамках.

Ну и разумеется, что идеально вписав все уже имеющиеся результаты в рамки, нельзя быть уверенным, что что-то не пойдет по звезде и результат вы не поймаете. Т.е. можно заранее увеличить M на некий процент и сидеть сжимая кулачки. Либо обработать вариант такого исхода в алгоритме.

[Сергей Соколов]

Termir988: вот про это число M и весь вопрос – как его посчитать? : )

[Limbend]

Сергей Соколов:
строишь сплайн,
смотришь максимальное отклонение от сплайна
думаешь
...

[Limbend]

Опишите ваше число, что это?
Оно постоянно растет?
Как часто бывают аномалии, явно выделяющиеся от сплайна?
Если это какая то активность пользователей, может стоит подумать о времени их активности, или... еще чего.

Людям из тостера не видно что у вас там происходит.

На данный момент ваш лучший вариант логарифмический поиск + максимально точный сплайн.

[Сергей Соколов]

Termir988: число это id создаваемых пользователями записей – сквозная нумерация. Пользователей миллионы, география широкая, часовые пояса, в основном, Россия, Европа. Т.е. суточные колебания есть, но они сглажены. И в то же время, это люди – а значит, теоретически, может быть как нулевое изменение числа записей с предыдущего момента, так и какой-то пиковый скачок при, скажем, заметных событиях. Поэтому никогда нельзя гарантировать, что выбранный для двоичного поиска диапазон (во всяком, его верхняя граница), захватит искомое значение. И вопрос – как расширять диапазон ?

[Сергей Соколов]

Рекомендация «подобрать число M таким, чтоб оно при любом раскладе охватило истинную величину» невыполнима. Есть ли алгоритм, похожий на двоичный поиск (кот. вы называете логарифмическим), только вывернутый наизнанку, вовне: как оптимально отодвигать границу поиска, если искомое не попало в изначальный диапазон?

[Limbend]

Сергей Соколов: отлично.
Ваша задача - минимизировать количество запросов.
Основное правило (... и нет, многие ему не следуют) не проверять уже проверенные значение.

0. Если число не может упасть, тогда стоит держать "под рукой" как минимум последнюю проверку (назову ее n0) и ниже нее уже не проверять.

1. Проверить [N+M; N-M] Если только N-M !< n0
Если нет в [N+M; N-M] то проверить [N-M; n0]
Если и там нет - это аномальный скачек. (или плохой расчет M) -> проверять [N+M; N+M+G] где G любое положительное число. Как и M расчет G задача ваша. Логика такая G = Nmax/2. Где Nmax - уж точно максимальное число пользователей. Пусть хоть "Over9000"/2.

2. Все таки найдя отрезок ищем в нем, деля его по полам.
Так же не нарушаем основное правило. Если в одной половине нет числа, то оно точно есть во второй. Не нужно ее проверять.

Поправка
G = Nmax/2 - M - N

А еще лучше
G = Nmax/2
А искать не в [N+M; N+M+G], а [N+M; G]
О - Оптимизация =)

Answer 2

[Сергей]

Гугл: Аппроксимация.
Экстраполяция.

Comments

[Сергей Соколов]

ок, вопрос про оптимизацию экстраполяции.

[Сергей]

> как правильно выполнять поиск методом научного тыка, если построить-таки модель, вписывающуюся в исторические данные, чтобы минизировать число тыков?
Я бы переформулировал: чтобы инртервал между тыками был максимальный, но при этом точность предсказанных измерений также максимальная.
Я бы начал с составления оценочной функции, которая бы давала оценку текущей ситуации (учитывая стоимость вызова, и точность предсказания).
Далее необходимо найти модель изменения максимума вашей постоянно растущей величины.
Ну и оперирую оценочной функцией подобрать такие интервалы тыка, чтобы оценочная функция были минимальна.