В общем виде задача такая:
Нужно найти на ненаправленном графе с неотрицательными весами ребер и узлов кратчайший путь не нарушающий определенных правил. Определить нарушает ли путь правила можно с помощью некой булевой функции isValid(Subpath x) которая на вход принимает путь целиком или его часть. Если часть пути невалидна, то не валиден и весь путь.
Пример 1:
Найти кратчайший путь, в котором ребра или ноды с определенным значением какого-то признака не встречаются более N раз подряд.
Пример 2:
Найти кратчайший путь, в котором ноды не должны быть включены в каком-то определенном порядке.
Первое что пришло в голову - взять алгоритм Дейкстры и добавить вызов isValid перед тем как считать вес подпути. Если подпуть невалиден - отбраковываем его. Это работает на простых примерах, но в принципе подход неправильный.
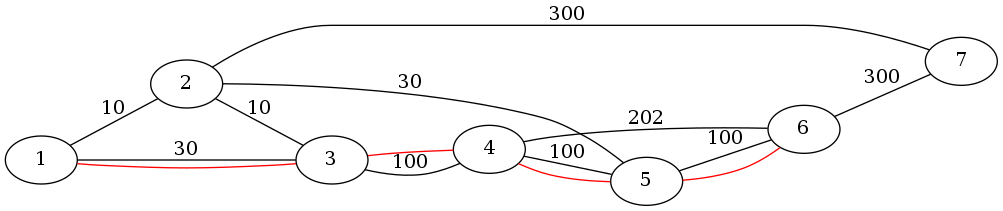
Например, имеем граф представленный на картинке, ищем путь от 1 до 6, веса написаны на ребрах. Допустим, что есть некие правила запрещающие, чтоб в пути были ноды в порядке 1-2-3 и 1-2-5.
По алгоритму Дейкстры с фильтрацией подпутей найдем путь 1-3-4-5-6 суммарной ценой 330, хотя кратчайший путь: 1-3-2-5-6, суммарной ценой 170.
Еще один вариант: использовать
алгоритм Йена но поменять условие выхода из внешнего цикла: искать не K путей, а первый путь для которого isValid == true. Так работать должно, но велика сложность алгоритма, будут проблемы с временем работы.
Может быть кто-то знает какие-то готовые решения, задача-то не такая уж и экзотическая.
