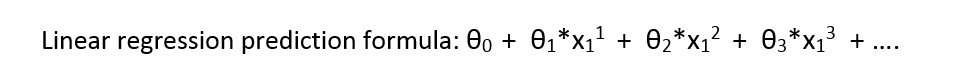Представление категорических и порядковых данных линейной регрессии (машинное обучение)?

Question

[Chichi]

Я пытаюсь полностью разобраться в разнице между представлением данных категорического и порядкового типов при выполнении регрессии. На данный момент существуют следующие правила:

Категорическая переменная и пример:
Цвет: красный, белый, черный
Почему категорическая: красный < белый < черный логически неверно

Порядковая переменная и пример:
Состояние: старый, реставрированный, новый
Почему порядковая: старый < реставрированный < новый логически верно

Методы перевода категорических и порядковых данных в численный формат:
Прямое кодирование (отображение) для категорических данных
Порядковое представление для порядковых данных.

Пример перевода категорических данных в числа:
data = {'color': ['blue', 'green', 'green', 'red']}

Численный формат:

id          Blue       Green      Red
0           1            0          0
1           0            1          0
2           0            1          0
3           0            0          1

Пример перевода порядковых данных в числа:
data = {'con': ['old', 'new', 'new', 'renovated']}

Численный формат после порядкового сопоставления: Старый < Реставрированный < Новый → 0, 1, 2

id  Data
0    0
1    2
2    2
3    1

В моих данных я имею свойство "цвет". Если цвет меняется от белого к черному то цена повышается. Из вышеуказанных правил представления данных я вероятно должен использовать прямое кодирование для своей категорической переменной. Но я не могу понять почему я не могу использовать порядковое представление. Ниже я представил свои наблюдения из которых у меня и возник вопрос.

Для начала представлю формулу линейной регрессии:


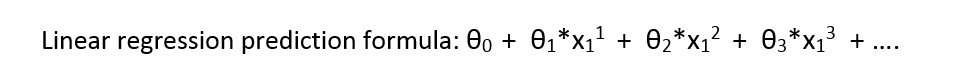
Теперь посмотрим на различное представление данных для свойства "цвет"

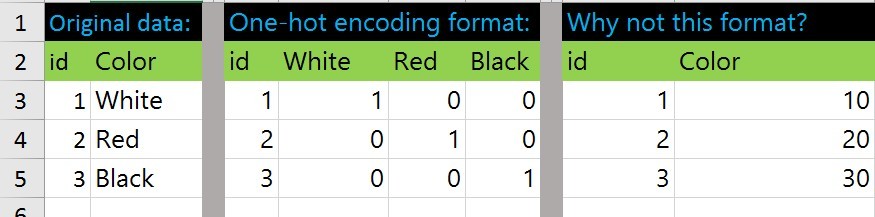
На картинке One-hot encoding - это прямое кодирование. А дальше это мое порядковое кодирование.

Теперь попробуем спрогнозировать цену для 1 и 2 элемента данных используя формулу для обоих представлений:

Прямое кодирование:
В этом случае будут разные Theta (коэффициенты) для различных цветов. Для примера я предположил что все коэффициенты определены (20, 50, 100) для трех цветов. Прогноз будет таким:
Цена (1-й элемент) = 0 + 20*1 + 50*0 + 100*0 = 20$
Цена (2-й элемент) = 0 + 20*0 + 50*1 + 100*0 = 50$

Порядковое кодирование:
В этом случае все цвета буду иметь общую Theta (коэффициент) но различные множители (мои порядковые коды). Прогноз будет выглядеть:
Цена (1-й элемент) = 0 + 20*10 = 200$
Цена (2-й элемент) = 0 + 20*20 = 400$

В моей модели Белый < Красный < Черный с точки зрения цены. Кажется что корреляция в обоих случаях работает и прогнозы выглядят логичными для порядкового и категорического представления. То есть получается независимо от того какой тип данных я использую (порядковый или категорический) я могу использовать любой метод перевода данных в численный формат? И это разделение на два типа больше представляет собой следование сложившимся соглашениям и более компьютеро-ориентированное представление чем проблему логики самой регрессии. В обоих случаях будет правильная модель регрессии?

Comments

[d'Ivan]

Поясни, пожалуйста, логику:
> Почему порядковая: старый < реставрированный < новый логически верно
Я не согласен с этим утверждением. Нельзя замерить количественно разницу между этими состояниями.

Answer 1

[SeptiM]

1. По сути вся машинка сводится к решению оптимизационных задач. Есть набор ограничений и есть функция, которую надо оптимизировать (min, max). В вашем случае вы, скорее всего, минимизируете среднеквадратическое отклонение. Делите выборку на две части, обучаетесь на тренировочной, считаете значение на контрольной. Вот это значение и есть критерий качества вашей модели.

2. Если есть несколько моделей и непонятно какую выбрать. Нужно поделить выборку на три части. На первой части мы тренируем модели, на второй -- выбираем модель с наилучшим показателем, на третьей -- получаем значение оптимизируемой функции на победителе предыдущей части, тот самый критерий качества.

3. Вывод: теория -- это хорошо, но лучше честно сравнить модели по данным.

4. Теория. Если вы представляете одну категорию несколькими переменными, то у вас получается большая размерность. На примере, если цвет вносит вклад по принципу белый -- 0, красный -- 10, черный -- 20, то в одной модели это будет 10 * x_цвет, а в другой 0 * x_белый + 10 * x_красный + 20 * x_черный. В то же время ситуация выглядит как белый -- 0, красный -- 10, черный -- 100, то в первой модели точного представления уже не получится, а во второй можно по прежнему расставить соответствующие веса.

По сути модель с множеством переменных является обобщением модели с одной. Проблема только, что число переменных растет...