Как найти наикратчайшие пути взвешенного орграфа, представленного матрицей инцидентности, используя алгоритм Дейкстры?

Question

[Cod Rob]

В интернете, к сожалению, я нашёл только алгоритм Дейкстры для матрицы смежности, но нигде нету алгоритма Дейкстры для матрицы инцидентности.
Моя матрица инцидентности (первый ряд цифр - номера вершин, то, что в {} - рёбра, всё остальное - вес; например, ребро {1;3} с весом 5 инцидентно вершине 3):
0 1 2 3 4 5 6 7
{0;1} 0 1 0 0 0 0 0 0
{0;2} 0 0 2 0 0 0 0 0
{1;2} 0 0 1 0 0 0 0 0
{1;3} 0 0 0 5 0 0 0 0
{1;4} 0 0 0 0 2 0 0 0
{2;3} 0 0 0 2 0 0 0 0
{2;4} 0 0 0 0 1 0 0 0
{2;5} 0 0 0 0 0 4 0 0
{3;4} 0 0 0 0 3 0 0 0
{3;5} 0 0 0 0 0 6 0 0
{3;6} 0 0 0 0 0 0 8 0
{4;5} 0 0 0 0 0 3 0 0
{4;6} 0 0 0 0 0 0 7 0
{5;6} 0 0 0 0 0 0 5 0
{5;7} 0 0 0 0 0 0 0 2
{6;7} 0 0 0 0 0 0 0 6
Для такого взвешенного орграфа:

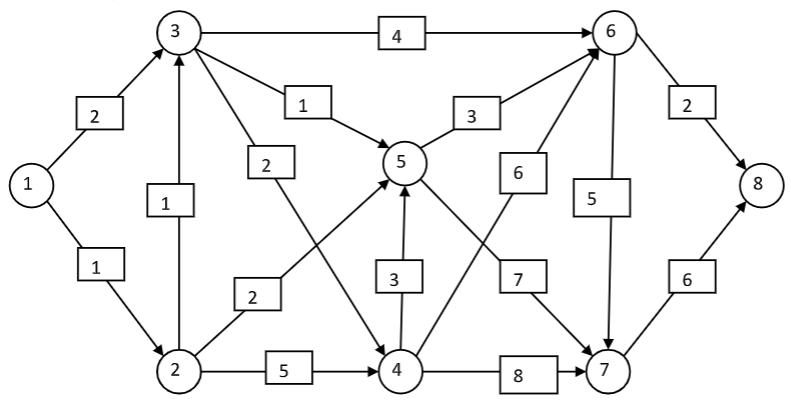
В прямоугольниках - вес ребра, а в кружках просто номера вершин, не вес.
Я пытаюсь написать алгоритм, который через алгоритм Дейкстры выведет наикратчайшие пути от введённой с клавиатуры вершины до всех других, то есть должно выводится вес пути и сам путь (вершины, через которые проходит этот путь).
Буду благодарен, если поможете с написанием алгоритма =)
На всякий: матрицу я представляю через вектор в коде:

vector<vector<int>> incidenceMatrix = {
	{0,1,0,0,0,0,0,0},
	{0,0,2,0,0,0,0,0},
	{0,0,1,0,0,0,0,0},
	{0,0,0,5,0,0,0,0},
	{0,0,0,0,2,0,0,0},
	{0,0,0,2,0,0,0,0},
	{0,0,0,0,1,0,0,0},
	{0,0,0,0,0,4,0,0},
	{0,0,0,0,3,0,0,0},
	{0,0,0,0,0,6,0,0},
	{0,0,0,0,0,0,8,0},
	{0,0,0,0,0,3,0,0},
	{0,0,0,0,0,0,7,0},
	{0,0,0,0,0,0,5,0},
	{0,0,0,0,0,0,0,2},
	{0,0,0,0,0,0,0,6},
};

Comments

[mayton2019]

Покажи что ты уже написал на С++.

[Cod Rob]

mayton2019, я пока что ничего не написал... только функцию вывода этой матрицы в нужном мне виде

[mayton2019]

Смотри. Дейкстра реализован уже миллион раз на всяких языках. Ты можешь взять любую реализацию
и использовать. Странно что ты не нашел AI-чяты которые все знают и не спросил решение там.

Структура данных у тебя - странная. Но тебе нужно построить над ней (и вообще над любой структурой)
следующий интерфейс (примерно).

interface Graph {
    void set_label(int v, int distance);
    int get_label(int v);
    int distance(int v1,int v2); 
    vector<int> neighbors(int v);
    .....
}

И уже алгоритм Дейкстры сможет работать используя эти методы. И надо заложить возможность
устанавливать дистанцию до нужной вершины в бесконечность. Это может быть константа типа MAX_INT.

Answer 1

[Wataru]

Матрица инцидентности - абсолютно не эффективная структра представления графа практически для всех алгоритмов. Поэтому вы ее использование нигде найти и не можете.

Если уж такое задание и надо именно это делать, то берете любую реализацию алгоритма дейкстры, скажем, со списком смежности и ищите там то место, где происходит перебор всех соседних вершин. И переписываете его: Чтобы найти все соседние вершины, вам надо пройтись по списку всех ребер и, если в матрице в столбце текущей вершины стоит отрицательное число, то ищите в этой строке положительное число - и вот тот столбец это и есть соседняя вершина.

Кстати, у вас матрица инцидентности неправильная: должно быть по 2 числа в каждой строке. Обычно ставят -цену у начальной вершины и +цену у конечной.

Comments

[Cod Rob]

Ох, понял, благодарю! Можно вас попросить, пожалуйста, показать, как тогда должна выглядеть матрица инцидентности? Нам просто на лекции рассказывали одно, а тут оказывается другое...

[Cod Rob]

И подскажите, пожалуйста, смогу ли я найти в интернете алгоритм Дейкстры для представления графа в виде списка рёбер? Просто мне по заданию разрешено использовать либо список рёбер, либо матрицу инцидентности... с матрицой смежности я уже реализовал всё, что нужно

[Wataru]

Cod Rob, Вот как матрица выглядит по-нормальному.

Со списком ребер, наверно, что-нибудь да найдете.

[Cod Rob]

Wataru, понял, благодарю!

Answer 2

[Alexandroppolus]

Переделай матрицу инцидентности в матрицу смежности

Comments

[Cod Rob]

К сожалению, мне по заданию разрешено использовать либо список рёбер, либо матрицу инцидентности... с матрицой смежности я уже реализовал всё, что нужно