Где могла закрасться ошибка?

Question

[floppa322]

Проблема: Есть обычная турнирная сетка на 8 человек. Также есть 2 человека A и B. Какова вероятность, что они встретятся на одной из игр?


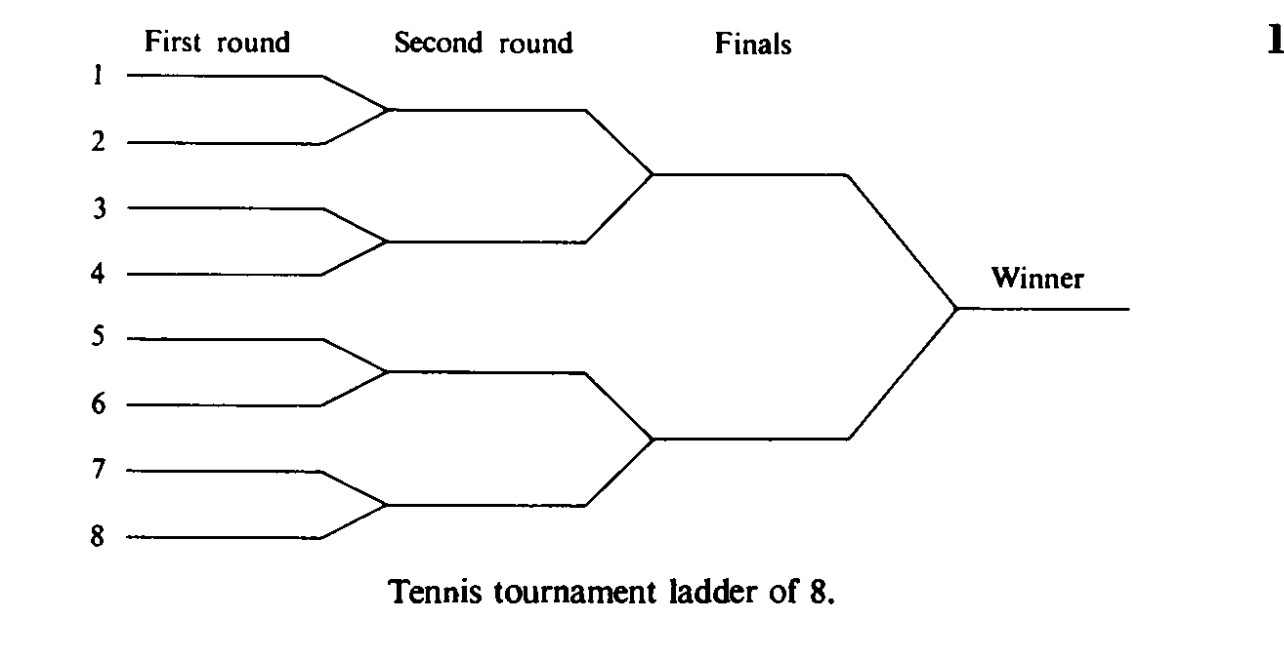
Решение автора: Шанс, что игрок A встретится с B в первом круге 1/7, шанс, что A и B встретятся во втором круге 2/7 * 1/4 (1/4 - каждый из них победит: 1/2 * 1/2) и шанс что они встретятся на последнем круге 4/7 * 1/16.
Итого: 1/7 + 2/7 * 1/4 + 4/7 * 1/16 = 0.25

Моё решение: Второе слагаемое - 2/7 * 1/4 посчитано неверно: если они встретились во втором круге турнира, то это значит что они не встретились в первом, а если они не встретились в первом, это значит, что если игрок A был на позиции 1, то игрок B должен быть на позициях [3;8] всего 6 позиций, игрок B не может находиться на позиции 2 потому что по условной вероятности, они не встретились (то есть позиция 1 по усл. вероятности закрыта игроком A, а позиция 2 по усл. вероятности невозможна, потому что у нас есть информация, что они оба победили, а значит 2-я недоступна), а значит слагаемое должно было быть 2/6, и итоговый ответ такой: 1/7 * 1 + 2/6 * 1/4 + 1/2 * 1/16 = 0.25744047619

Просимулировав для уверенности данную проблему, выяснил, что вероятность всё-таки 0.25. Код симуляции
Где я мог ошибиться в своих рассуждения ?

P.S.: когда решал через комбинаторику, а не усл. вероятность, то получил 0.25

Comments

[floppa322]

Несовсем понял, почему тег сменили с математики на алгоритмы, когда в вопросе представлена задача по теории вероятности, неужели потому что в тексте есть ссылка на код

Answer 1

[Wataru]

В вашем рассуждении ошибка в том, что вы не домножаете условную вероятность 2/6 на вероятность условия. Вы же полную вероятность считатете а P(A) = P(A|B)*P(B)+P(A|!B)*P(!B). У вас P(A|B) = 0, как вы заметили - если они встретились в первом туре, то во втором уже не встретятся. Но все-равно надо 2/6 домножать на P(!B) - вероятность того, что они не встретились в первом туре. А это 1-1/7 = 6/7. В итоге получается все то же 2/6*6/7=2/7.

Но рассуждения автора проще. Можно рассмотреть все независимые элементарные исходы "где в сетке оказался второй игрок". Их 7, они равновероятны по симметрии. Дальше надо домножить на вероятность, что они начиная так встретятся (выиграют свои матчи).

Comments

[floppa322]

Спасибо за ответ :)

[floppa322]

Кстати, всегда мучил следующий вопрос в теории вероятностей: вот тут есть 3 способа решить эту задачу:
1. Через комбинаторику (достаточно легко запутаться, но можно)
2. Через условную вероятность + умножение вероятностей (тоже легко что-то не учесть, но попроще, чем 1-й способ)
3. Через умножение вероятностей (хотя умножение, насколько я понимаю выводится из усл. вероятности, которая является вообще аксиомой)

Все эти 3 модели опираются на некоторые простые факты:
1-й способ на равновероятность всех возможных игр и классическую формулу вероятности;
2-й способ на теорему усл. вероятности, умножение вероятностей, классическую формулу вероятности
3-й способ на умножение вероятностей, классическую формулу вероятности

При этом у этих 3-х моделей, казалось бы, совсем непохожих, одинаковый результат при довольно нетрривиальных вычислениях.
И любопытно: есть ли у этих 3-х моделей под собой какая-то единая база (как, например, в геометрии). Ну вот, например, у 2-го и 3-го способа вроде бы есть, а вот у 1-го и 2,3-х способов уже довольно затруднительно сказать. Хотя я вот для себя это понимаю (что 3 модели дают одинаковый результат) просто, что у них у всех в конечном счёте одинаковые меры множества

[Wataru]

floppa322, Комбинаторика сама по себе ответа никакого не даст. Она лишь поможет посчитать элементарные исходы. Условная вероятность тоже в итоге считает элементарные исходы, но иногда через нее проще рассуждать. Но по сути это все одно и то же: чтобы подсчитать вероятность события, надо взять количество благоприятных исходов и поделить на общее количество исходов.
Вот как есть у вас геометрическая задача и вам надо подсчитать площадь заштрихованной области. Можно разными способами пилить искомую область на части. Но итог один.
Вот в задачах на вероятность у вас тоже есть картинка - только многомерная и дискретная - где какая-то область заштрихована и вы тоже ищите ее "площадь". Условная вероятность - это вы берете и считаете площать фигуры как площадь какой-то другой фигуры минус лишнее. Комбинаторика - это как бы интеграл для подсчета площади. Классическая формула - это разбить на удобно считаемые части и отдельно каждую подсчитать.

[floppa322]

Wataru, спасибо, довольно неплохая метафора с площадью

Answer 2

[Alexandroppolus]

Если взять турнирную сетку на 2^N человек (или N раундов), то можно ещё составить рекуррентную формулу вероятности встречи P(N)

P(1) = 1
P(N) = 1/(2^N - 1) + (2^N - 2) /(2^N - 1) * 1/4 * P(N-1)

2^N - это 2 в степени N

здесь первое слагаемое для случая, когда второй игрок в самом ближайшем раунде встречается с первым
второе слагаемое - все остальные случаи, для которых с вероятностью 1/4 оба игрока выиграют раунд и далее встретятся с вероятностью P(N-1)

теперь по индукции можно доказать, что P(N) = 1/2^(N-1)