Ну все ли вы делаете правильно это совершенно неизвестно, (Это большой вопрос как сделана выборка, что за данные и т.д. вообщем соблюдены ли все условия) и так сходу не ответишь Это надо сидеть и разбираться (иметь ваши данные и время (сразу скажу делать я этого не буду)). А вот на остальное ответить вполне себе можно.
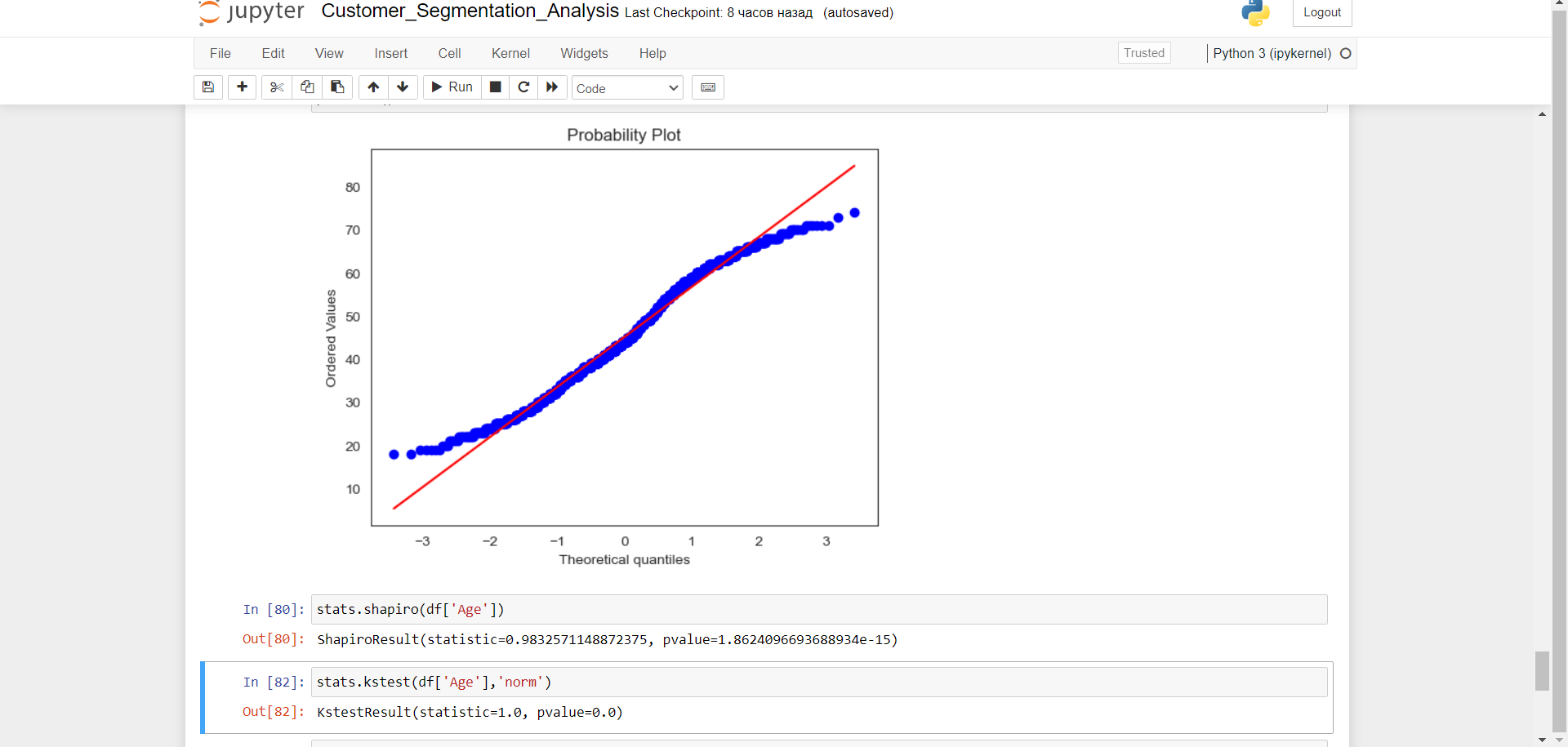
1. График о чем говорит? Нормальное распределение подразумевает, крайне маленькие вероятности у "хвостов" распределения, то есть если вы отклонились более 2 стандартных отклонений то там 5 процентов всего по 2.5 с каждого края, на вашем же графике далекие от среднего значения НЕ являются маловероятными событиями. В статистике это называется fat tails. То есть это не НОРМАЛЬНОЕ распределение не будет такого что 95 процентов лежат в пределах двух стандартных отклонений, это значение будет меньше (Экстремальные величины не являются маловероятными).
2. По поводу теста тут все просто. Что такое p-value? Это вероятность тестовой статистики при условии НУЛЕВАЯ Гипотеза ИСТИННА. Поговорим о логике эксперемента. Допустим мы говорим средний рост прохожего (мужского) пола 175см. Это ПАРАМЕТР популяции который мы хотим затестить посредством СЛУЧАЙНОЙ выборки. Мы выходим на улицу берем 500 (например дизайн эксперемента я опускаю) мужчин измеряем их рост и берем среднее значение это ТЕСТОВАЯ статистика, далее мы нормализуем (трансформируем наши ТЕСТОВУЮ статистику после чего она измерятся не в см а в стандартных отклонениях) ну и находим вероятность ТЕСТОВОЙ статистике из такого распределения где ПАРАМЕТР истинен. Если это вероятность ниже установленного заранее порога, мы отвергаем нулевую гипотезу. Потому что мы говорим это очень маловероятно видеть такую ТЕСТОВУЮ статистику при условии нулевой гипотезы истинной. Это общая направление ИДЕЯ. Частные имплементации могут отличаться в зависимости сколько данных у нас есть что мы знаем о распределении популяции и .т.д. Это была общая логика.
У теста Колмагорова-Смирнова есть своя формула для ТЕСТОВОЙ Статистики которая показывает своего рода "дистанцию" между распределением выборки и в данном случае нормальным распределением (Упрощенно читайте подробнее) и вычисляет ее вероятность. В вашем случае он вам показал что вероятность равна нулю. (То есть уверенно отвергаем нулевую гипотезу).
Это что можно понять из предоставленной вами информации, повторюсь ответить правильно ли вы все сделали возможности нет.