Как решить олимпиадную задачу с графами?

Question

[Марат Нагаев]

Есть граф. Нужно найти кратчайший путь из точки A в конец.
В некоторых вершинах графа есть награды, которые нужно собрать кратчайшим способом.
Какой алгоритм лучше применить и как?
Полное условие:
Городок Еловый славится своими двумя вещами — здесь каждую неделю Новый год и везде очень узкие дороги. Если с первым еще можно как-то бороться, то со вторым городу очень тяжело. Именно поэтому жителям нужна Ваша помощь!

Вам дана карта города Еловый. Как ни странно, он очень похож по форме на елку. Елью в данной задаче будем называть неориентированный граф, состоящий из цикла, к которому присоединён черенок, представляющий собой несколько последовательно связанных рёбер. Самую отдалённую от цикла вершину черенка будем называть корнем ели. В корне находится выезд из города. На некоторых улицах города с последнего Нового года лежат ёлки, которые надо вывезти из города.

Необходимо помочь уборочной машине убрать все елки из городка, пока не наступил Новый год! Ведь начинать новую неделю Нового года со старой елкой является плохой приметой в этом городе. Вы можете выбрать любую вершину графа в качестве стартовой точки, но главным условием является закончить сбор елок на выезде из города, иначе елки вывезти не удастся, ведь разворачиваться на узкой дороге нельзя, не правда ли? Так же, вы не можете посещать одну вершину несколько раз — мэр города, который построил такие дороги точно уверен, что есть более оптимальный маршрут для сбора елок!

Елки ждут!

Comments

[Сергей П]

А вы самостоятельно искать решение пробовали? Какие делали попытки? Что у вас не получилось? Вам нужно готовое рещение тут, или что?

[Марат Нагаев]

Сергей Паньков, желательно готовое решение
хотя бы простое объяснение на словах что нужно использовать такой то алгоритм и так-то
Я пробовал Дейкстрой решить, но не вышло.

[Wataru]

Марат Нагаев Дайте уж лучше ссылку на условие. Пока ничего не понятно. Как считаются награды? Собрать все? Или они численные и суммируются? Какие ограничения? Сколько вершин, сколько ребер сколько наград, ребра все одинаковой длины или разной? Есть ли отрицательные ребра в графе? Граф вообще ориентированный или нет? Может он дерево? Что важнее: кратчайший путь из A в конец, или собрать все награды? Ведь ради наград придется делать крюки и удлинять путь.

Разные ответы на эти вопросы делают задачу принципиально разной. Где-то сработает дейкстра, где-то может сработать динамическое программирование, а где-то только полный перебор или какая-то дичь вроде метода отжига.

[Alexandroppolus]

В некоторых вершинах графа есть награды, которые нужно собрать кратчайшим способом.

выглядит как "задача коммивояжера"

[Марат Нагаев]

Wataru, добавил в описание

[YaKotikTvoy]

Точно скажу, что нужно использовать DFS алгоритм, то есть поиск вглубь.

Answer 1

[Wataru]

Поскольку тут очень специфический граф - тут не надо никаких алгоритмов для графов. Это задача тупо на разбор случаев. Единственные возможные маршруты в этом графе - начать с какой-то вершины цикла и поехать вправо или влево, пока не доедете до черенка, и дальше по нему к выезду. Или можно начать на черенке и уехать. Очевидно, что первые два варианта - это надо начать с ближайшей к черенку елки в каждую сторону и поехать в ту же сторону дальше. Длина маршрута - количестов ребер минус рассотяние от елки до черенка в данную сторону. Третий путь можно начать на ближайшей к циклу елке на черенке и ехать на выход. Первые 2 варианта - если есть елки на цикле, третий вариант - если нет.

Вам надо только понять какие вершины в цикле, а какие на черенке. Тут можно обходом в глубину или ширину это найти. Или даже тупо циклом. В графе есть одна вершина степени 1 - она же выезд. От нее надо идти к соседним, пока не дойдете до единственной вершины степени 3. Пройденные так вершины будут черенком. Остальные - в цикле.

А дальше вам надо посчитать длины трех маршрутов и выбрать из них лучший.

Answer 2

[YaKotikTvoy]

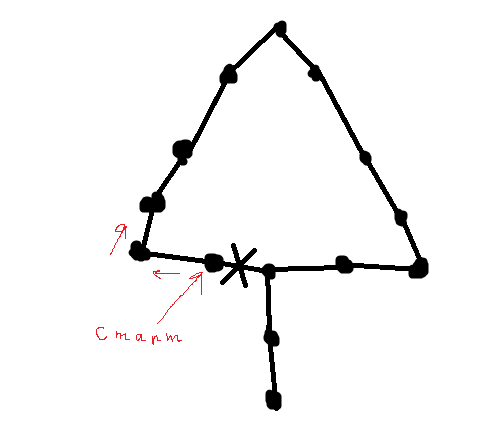
Здесь вам нужно найти остовное дерево графа, да притом такое, что его можно выпрямить. Но так как, там по сути, как я понял, просто цикл, а ещё есть одно тупиковое ответвление, то вам просто нужно взять и запустить DFS, либо BFS алгоритм с точки, которая около черенка.
Для того, чтобы BFS или DFS сразу не пошли к черенку, удалите ребро ведущую к выходу, то есть тупику, но при этом подразумеваете, что оно есть , это уже и будет то минимальное расстояние, остовное дерево.
Запишите этот путь в массив или множество и задача решена.

Вот DFS, припишите то, что нужно для записи пути и выведите его.

N,M = [int(i) for i in input().split()]
G = {}
for i in V:
    if i not in used:
            t += 1
            dfs(i,G,used)

N, M - количество вершин и ребер соответственно.
Все ребра и вершины необходимо прописать самому.
В данном случае, лучше DFS (поиск в глубину).

Comments

[Марат Нагаев]

Спасибо!

[YaKotikTvoy]

Марат Нагаев, Там V у меня не прописано :), V-множество вершин, но думаю додумаетесь, как всё это записать.

[YaKotikTvoy]

Ещё я вам DFS забыл кинуть :) вот его реализация на Python

def dfs(vertex, G, used):
    used.add(vertex)
    for n in G[vertex]:
        if n not in used:
            dfs(n,G,used)

[Wataru]

Артём Сединин, @nagayev
Ну тут не надо dfs вообще. Зачем стек наматывать, если можно просто циклом пройтись, если помнить соседнюю вершину.

p = trunk_base # вершина из которой растет черенок
v = <next vertex> # соседняя вершина к p вдоль цикла
while power[v] != 3:
  for n in G[v]:
    if n != p:
      v = n
      p = v
      break

Аналогично можно пройтись по всем вершинам в черенке.