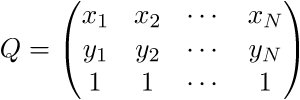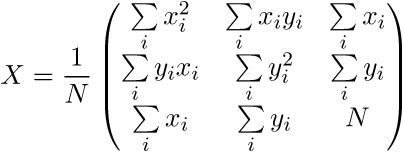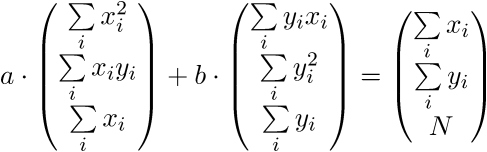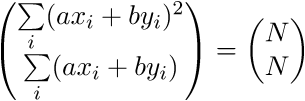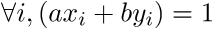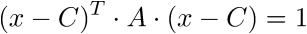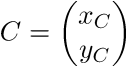Whiteha

Проблема 1:

Матрица Q имеет вид:



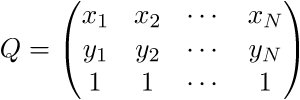
Матрица X имеет вид:



С учетом вида матрицы Q матрица X примет вид:



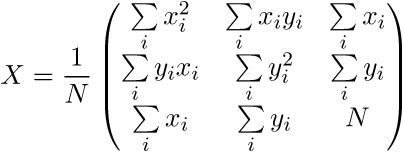
Если все x или y равны нулю, то все точки лежат на одной прямой. Это частный неинтересный случай. Если есть x и y ненулевые, то у нас не будет нулевых строк. Если определитель матрицы X равен нулю, то можно написать (выразить строки через друг друга; более простые случаи очевидны):



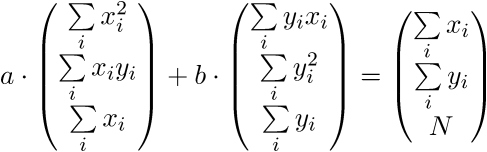
Тоже самое:



Домножаем первую строку на a, вторую на b, складываем:



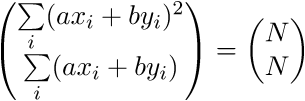
Такая точка (в пространстве размерности N) единственна, при



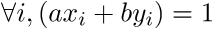
Это очевидно для случая N = 2. Нарисуйте круг с квадратом радиуса равным 2 и прямую x + y = 2. Они будут касаться в одной точке. После того как нарисуете, это станет очевидно и для любого N.

Итак, мы доказали, что если определитель X равен нулю, то точки лежат на одной прямой.

Проблема 2:

C сайта матлаба нашел правую часть:



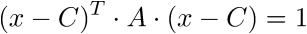
Нужно найти собственные значения и собственные вектора единичной длины (они должны быть ортогональны) для матрицы A, после чего используя точку



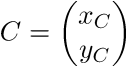
как центр, нужно провести собственный вектор длиной



(лямбда соответствует собственному вектору). Аналагично для другого. Эти вектора будут большой и малой полуосями для нашего эллипса. Дальше по возможностям визуализатора.

Как-то все сумбурно получилось.

В https://sqlite.org/fts5.html#section_7_1 ясно написано:

xTokenize:
This function is expected to tokenize the nText byte string indicated by argument pText. pText may or may not be nul-terminated. The first argument passed to this function is a pointer to an Fts5Tokenizer object returned by an earlier call to xCreate().
..........
For each token in the input string, the supplied callback xToken() must be invoked.

ВЫ пишете тройку функций xCreate, xDelete, xTokenize. При вызове вашей xTokenize ей будет передан колбэк, который, как правильно подметил abcd0x00 , нужно будет дергать для передачи движку SQLite готовой (т.е. подготовленной ВАМИ в процессе работы xTokenize) лексемы. Они называют это токен, но вообще это лексема, т.к. вы отдаете кусок из входной строки.
Итого, все максимально просто - вам дается строка, вы по своим алгоритмам и критериям решаете, где в ней какие лексемы. Для каждой найденной лексемы дергаете данный вам xToken, чтобы сообщить эту радостную новость SQLite.

Обязаны ли мы его вызывать?

нет, но если не будете вызывать, ни одной лексемы из входной строки SQLite не получит.

Если его должны реализовать мы

его реализует SQLite.

В кратце, желательно, чтобы в массиве дискретизации было целое количество периодов входного сигнала, иначе необходимо накладывать окно, с целью минимизации краевых эффектов. Далее сделать преобразование Гильберта, найти ортогональный сигнал, после чего найти огибающую: A[iTд]=sqrt(Uг[iТд]^2+Uф[[iТд]^2), где Uг[iТд] ортогональный сигнал, а Uф[[iТд]- ваш исходный.