Как замостить ориентированный по осям Rectangle блоками максимального размера, обходя препятствия?

Question

[wlastas]

Доброго дня.
Задача поиска пути и возможности атаковать (отсутствие препятствий в заданном направлении на нужном расстоянии) - нужна оптимизация построения условного Navigation mesh .
Есть большая готовая сетка проходимости(бывают до 1000х1000), разбитая на "квадраты 8x8" с непроходимыми секторами (красные на картинках).
Комбинируя проходимые сектора(1х1) внутри "квадратов 8x8" я строю грани navmesh, центры которых использую в качестве узлов графа.
Простое решение, которое работает сейчас, это разбиение "квадрата 8x8" на полоски 1хN,

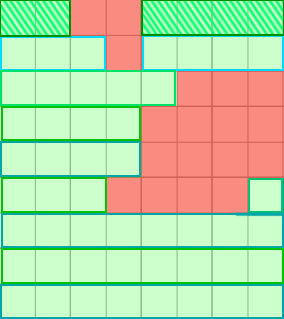
но это немного медленно - хотелось бы ускорить в 2-4 раза.

Скорее всего будет отлично работать вариант как тут:

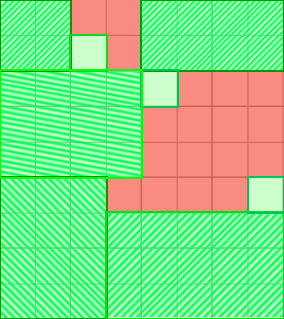
Подскажите алгоритм ( может есть какая-то готовая математическая реализация), который можно использовать, чтобы получить проходимые сектора максимального размера

Comments

[Армянское Радио]

Я прочитал задание примерно 8 раз и ничего не понял из-за противоречия:

1) У вас отобраны проходимые и непроходимые секторы.

2) Далее, вы начинаете искать в непроходимом секторе проходимую грань. Как так-то?

[wlastas]

2) Далее, вы начинаете искать в непроходимом секторе проходимую грань. Как так-то?

Я в квадратах 8х8 ищу и строю грани из секторов 1х1, получая полоски 1xN - на картинках разве непонятно.
Ок перефразирую чтобы небыло неоднозначности с "в которых"

[Akina]

Скорее всего будет отлично работать вариант как тут:

Неоптимально поделено... можно уложиться в 7 плиток.

К слову, прилегание по стороне не гарантирует не-прохождения отрезка между центрами через запрещённую область.

[wlastas]

Неоптимально поделено... можно уложиться в 7 плиток.

да, вариантов может быть много, важно чтобы каждый из проходимых секторов был по возможности максимально большой площади.  По идее можно генерить несколько решений и выбирать оптимальное - важен алгоритм^^
Есть какие-нибудь идеи?

Answer 1

[Wataru]

Во-первых, не очень понятно, зачем вам вообще это. Агрегируя квадратики в прямоугольники вы будете находить не самые короткие пути в этом графе. Каким алгоритмом вы дальше в графе работаете? Какой-нибудь Jump point search на неаггрегированных клетках может быть быстрее чего-бы то нибыло по аггрегированным.

Далее, если вам так хочется, то ваша задача аггрегирования - NP и кроме полного перебора вы не найдете оптимальное решение. Но вам, похоже, подойдет какое-нибудь достаточно хорошее решение, а не только оптимальное. Тогда будут работать всякие жадности и эвристики. Можно, например, брать самую левую-верхнюю непокрытую клетку и жадно растить вокруг нее максимальный по площади прямоугольник, который не пересекает ни одну покрытую или запрещенную клетку (допустим, перебирая нижнюю и верхнюю границу и жадно раздувая левую и правую до максимума). На примере из вопроса этот алгоритм построит 7 прямоугольников.

Comments

[wlastas]

Во-первых, не очень понятно, зачем вам вообще это.

Текущий алгоритм с полосками используется помимо поиска пути так же и для отображения карты, посещённых регионов, зон опасности(что видят враги). Непроходимые полоски тестируются на предмет препятствия для прохождения и видимости/доступности(для прямолинейной удаленной атаки) целей за ними.
При большом размере карты и большом числе полосок прорисовка падает до 20 фпс - нужно до 4 раз сократить число вызовов ImGui....AddQuadFilled(..)

Поиск тут какой-то комбинированный/доработанный дейкстра кажется (ничего не понимаю в этих алгоритмах) - я взял готовое решение, с ним нет никаких проблем. 
В комментариях к коду ссылки на
https://en.wikipedia.org/wiki/2-opt
https://on-demand.gputechconf.com/gtc/2014/present...

[wlastas]

брать самую левую-верхнюю непокрытую клетку и жадно растить вокруг нее максимальный по площади...

Идею понял, спс - поробую так тоже

[wlastas]

по факту 10+ раз прирост в скорости отрисовки ;-))

Answer 2

[hint000]

Простое решение, которое работает сейчас, это разбиение "квадрата 8x8" на полоски 1хN,

Предложу легко реализуемое улучшение, хотя и НЕ гарантирующее оптимальности.
Берёте ваши готовые полоски 1хN. Если снизу или сверху к этой полоске примыкает полоска с такими же координатами начала и конца, то объединяете эти полоски. Продолжаете проверку, если к полученному блоку примыкает ещё такая же полоска, то и её присоединяем к блоку, и т.д.
Плюс в простоте.

На вашем примере это даст 8 блоков вместо 12 полосок.

Answer 3

[wlastas]

На вашем примере это даст 8 блоков вместо 12 полосок.

Да, спс, так получится 7 полосок и 2 блока. 
Еще есть вариант дополнительно нагенерить к этому же "квадрату 8х8" по такой же схеме, но на вертикальных полосах, и выбрать лучший. 
Насколько будет прирост от такой оптимизации - надо проверять.
Квадраты без препятствий внутри у меня и так не режутся на полосы и берутся как 8х8

Comments

[hint000]

так получится 7 полосок и 2 блока

5 полосок и 3 блока

[wlastas]

hint000, ах да вижу, правый верхний будет поймать сложнее
я хотел построчно идти сверху вниз и сверять новый блок с предыдущим, а так надо будет все блоки предыдущей строки сравнивать с каждым блоком текущей строки. 
Эх....