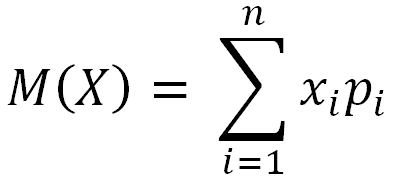Задача:
Word-ландия – новая страна, образованная объединением двух древних государств под воздействием внешних угроз. Эти государства теперь являются провинциями Word-ландии, но референдумы по их наименованию ещё не прошли, поэтому они называются Старшая и Младшая Byte-ландии.
Для сплочения населения было решено провести чемпионат между провинциями. В Старшей Byte-ландии национальной игрой являются шахматы, а в Младшей – волейбол. Поэтому чемпионат решили провести по шахболу. Чтобы не затягивать чемпионат, объединённое правительство решило провести ровно К матчей. Каждый матч – это либо партия в шахматы, либо волейбольный матч. Победитель в матче получает одно очко в зачёт чемпионата, в случае ничьей в шахматной партии обе провинции получают по 0.5 очка.
Правительство заинтересовано в том, чтобы в чемпионате «победила дружба», то есть провинции набрали одинаковое количество очков. Поэтому высокие чины обратились к вам с просьбой определения минимального количества шахматных партий в чемпионате, чтобы разность математических ожиданий набранных провинциями очков была минимальна.
За долгую историю Мировых чемпионатов известно, что Старшая Byte-ландия выигрывает в шахматы у Младшей с вероятностью p1 и проигрывает в волейбол с вероятностью p2. Ничья в шахматах достигалась с вероятностью p3. Примечание: Математическое ожидание - среднее значение случайной величины в теории вероятностей. Для дискретной случайной величины Х с законом распределения P(X = xi) = pi математическим ожиданием называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е.
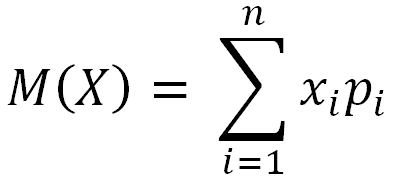Входные данные:
Входной файл INPUT.TXT содержит четыре целых числа: К (1 < K ≤ 10^16), p1, p2, p3 (0 ≤ p1, p2, p3 ≤ 100) – количества матчей и вероятностей в процентах.
Выходные данные:
В выходной файл OUTPUT.TXT выведите одно натуральное число – минимальное количество шахматных партий (учтите, что чемпионат не должен превратиться в шахматный турнир).
Примеры:
Вход:
3 50 50 50
Выход:
1
Вход:
4 0 0 100
Выход:
3
Идея: воспользоваться формулой и посчитать вероятность выигрышей для каждой команды, для ничьи не нужно, потому что она будет одинаковой для обоих команд и сократится при вычитании. Считать нужно для всех различных количеств игры в шахматы, но нельзя, чтобы играли только в шахматы. Потом выводим число партий, для которого модуль разности математического ожидания минимален.
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
struct Chess
{
long long int number;
long long int p1;
long long int p2;
long long int p3;
long double difference;
};
int main()
{
long long int aNumber = 0, pos1 = 0, pos2 = 0, pos3 = 0;
std::cin >> aNumber;
std::cin >> pos1;
std::cin >> pos2;
std::cin >> pos3;
std::vector<Chess> chess(aNumber);
for (long long int i = 0; i < aNumber; i++)
{
chess[i].number = i + 1;
chess[i].p1 = pos1;
chess[i].p2 = pos2;
chess[i].p3 = pos3;
chess[i].difference = abs(2 * chess[i].number * (chess[i].p1 + chess[i].p2 - 100) +
aNumber * (100 - 2 * chess[i].p2)
);
}
std::sort(chess.begin(), chess.end(), [](Chess& left, Chess& right)
{
return left.difference < right.difference;
});
if (chess[0].number == aNumber)
{
std::cout << chess[1].number;
}
else
{
std::cout << chess[0].number;
}
}
