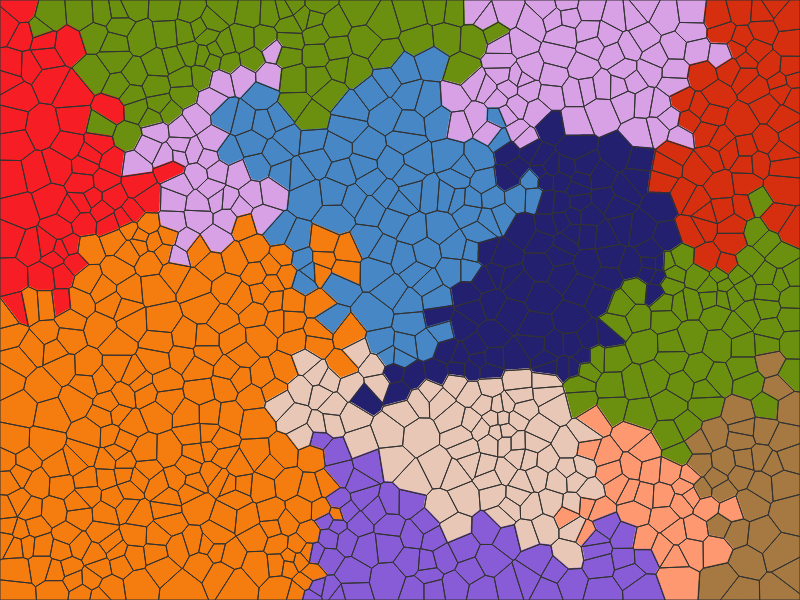
Вот упрощённый вариант "на пальцах":
import cv2
import numpy as np
from PIL import Image
from itertools import product
N = 42
W = 200
H = 200
def distance(p1, p2):
y1, x1 = p1
y2, x2 = p2
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
canvas = np.zeros((H, W, 3), dtype=np.uint8)
centers = np.unravel_index(np.random.randint(0, W * H, N), canvas.shape[:2])
canvas[centers] = np.random.randint(0, 256, (N, 3))
centers = list(zip(*centers))
for x in range(0, W):
for y in range(0, H):
cy, cx = min(centers, key=lambda center: distance(center, (y, x)))
canvas[y, x] = canvas[cy, cx]
Результат:

Для получения невыпуклых многоугольников можете случайным образом пообъединять смежные области. Например, берёте случайный центр, ищете ближайший к нему (или один из ближайших), закрашиваете области одним цветом, в списке центров вместо двух вставляете один. И так далее.