Как построить график функции в windows forms c#?

Question

[HEDAX]

Мне нужно нарисовать график функции циссоиды Диокла.

Так как я не очень понимаю как эту функцию вставить в windows forms c#, я использовал уравнение циссоиды в прямоугольной системе координат:

Вот мой код:

public Form1() {
			InitializeComponent();
			int a = 4, m;
			for (int i = 1; i<50; i++) {
				m = (((2 * a) - i) / 2);
				if (m == 0) {
					m = 1;
				}
				chart1.Series[0].Points.AddXY((i), (i*i*i)/m);
			}		
		}

К сожалению, получается совсем не то, что нужно:

Я думаю, что проблема в том, как я записываю функцию. Может ли кто-то помочь мне решить это?

Answer 1

[Александр Ананьев]

Дык, а корень кто будет извлекать?
А так у вас строится y=x*x*x/(2*a-x). Кстати, выражение знаменателя тоже зачем-то у вас делится на 2.

Comments

[HEDAX]

Я исправил на:
public Form1() {
InitializeComponent();
int a = 4, m;
for (int i = 1; i<50; i++) {
m = ((2 * a) - i);
if (m == 0) {
m = 1;
}
chart1.Series[0].Points.AddXY((i), ((i*i*i)/m)/2);
}
}
Но все равно получается не так, как нужно:

[Александр Ананьев]

HEDAX, Ну, а корень квадратный почему не извлекли?

Answer 2

[Foggy Finder]

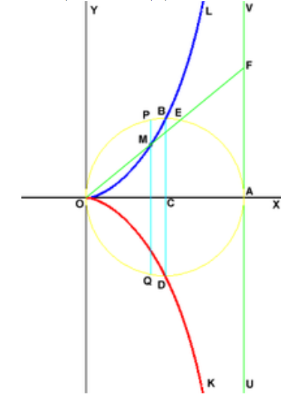
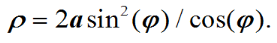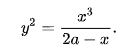Тут у вас сразу несколько ошибок:

1. Нужно явно приводить к double иначе при делении двух int получите тоже целое.
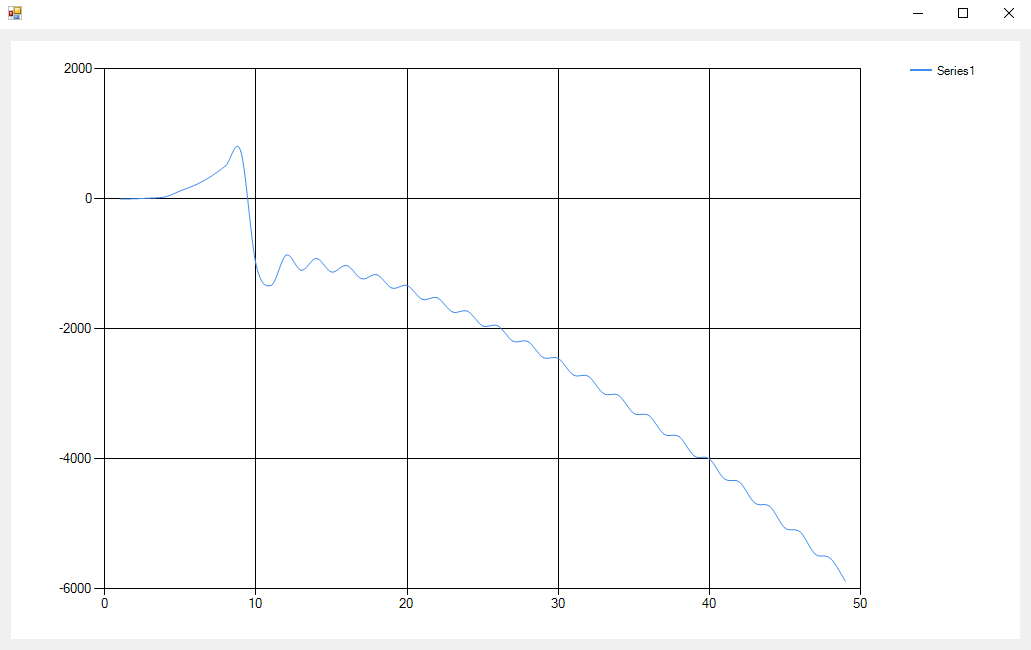
2. Вы берете очень большие границы. Рост знаменателя намного превышает скорость роста числителя. Сами посмотрите: возведите 50 в куб, что получите? График вы конечно построите, но наглядности будет немного.

Что более важно: ваш отрезок OA = 2*a, а это значит что ваша правая граница точно должна быть меньше чем 2*a;

3. Посмотрите как задана функция - в виде квадрата. Извлекая корень вы должны не забывать про нижнюю ветку - ту которую дают отрицательные значения y.
Насколько мне известно возможности стандартного контрола довольно ограничены - вам придется заносить значения во вторую линию.

Собирая все вместе, попробуйте что-то вроде такого:

double a = 3;
double step = 0.1;

for (double x = 0; x < 2 * a - 1; x += step)
{
    var n = x * x * x;
    var d = 2 * a - x;
    chart1.Series[0].Points.AddXY(x, Math.Sqrt(n / d));
    chart1.Series[1].Points.AddXY(x, -Math.Sqrt(n / d));
}

Здесь 1 (x < 2 * a - 1) вычитается только для примера, чтобы вы сравнили результат. В реальности вам придется определять границу более сложным путем чтобы для разных a и левой границы (x) получать наглядное представление. Но, по крайней мере, у вас есть от чего отталкиваться.