дополню ответ
rPman - поиск в ширину в данном случае является самым быстрым. Не совсем понимаю почему
Думал уже - долгий он!
, потому как сложность O(V+E), где V - количество вершин, а E - количество ребер; для данного случая V=70, E=138, вообще копейки. Может не совсем верно его понимаете?
Покажу как я делал - для начала построил список смежности для этого графа, пронумеровал вот так:
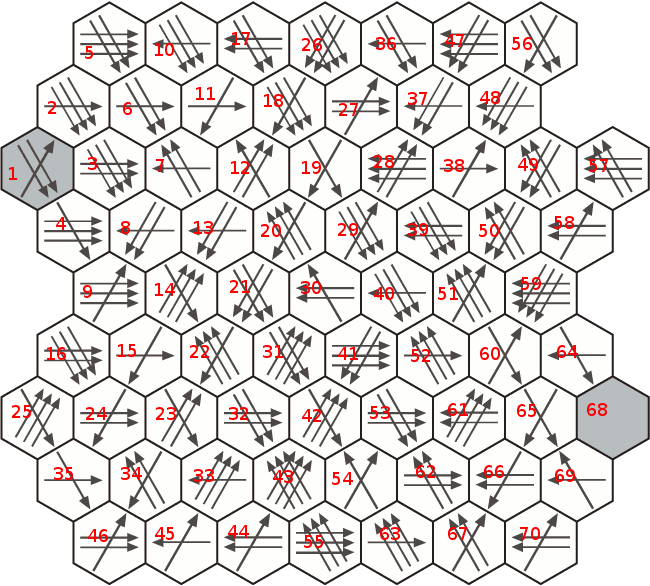
получился
список смежности1: 2 9
2: 6 14
3: 12 22
4: 9 20
5: 7 26
6: 11 13
7: 5 3
8: 4 16
9: 8 30
10: 5 20
11: 18 7
12: 11 26
13: 8 15
14: 22 18
15: 22 24
16: 22 45
17: 5 19
18: 12 40
19: 20 29
20: 21 10
21: 42 23
22: 23 3
23: 33 21
24: 32 35
25: 8 35
26: 12 39
27: 36 48
28: 47 7
29: 28 61
30: 20 14
31: 28 54
32: 55 53
33: 30 34
34: 46 16
35: 34 46
36: 38 26
37: 29 27
38: 48 49
39: 20 65
40: 30 66
41: 64 43
42: 54 39
43: 40 14
44: 43 46
45: 33 46
46: 34 44
47: 17 28
48: 40 37
49: 47 51
50: 37 52
51: 50 27
52: 60 19
53: 65 67
54: 53 42
55: 22 70
56: 48 57
57: 56 28
58: 57 39
59: 62 30
60: 59 65
61: 58 42
62: 41 69
63: 67 31
64: 68 60
65: 69 66
66: 67 54
67: 66 53
68:
69: 65 66
70: 69 63
и простая реализация bfs на ruby
data = File.read('input.txt').split("\n").map { |line| line.split(":") }.map {|item| [item[0].to_i, item[1].split(' ').map(&:to_i)]}.to_h
puts data # {1=>[2, 9], 2=>[6, 14], 3=>[12, 22], ...
queue = [1]
visited = [1]
prev_vertex = {1 => -1}
while queue.any?
vertex = queue.shift
data[vertex].each do |neightbor_vertex|
next if visited.include?(neightbor_vertex)
queue << neightbor_vertex
visited << neightbor_vertex
prev_vertex[neightbor_vertex] = vertex
end
end
vertex = 68
path = []
while vertex != -1
path << vertex
vertex = prev_vertex[vertex]
end
puts path.reverse
коду на этом графе надо 68 шагов для прохода вперед, и 35 обратно (для построения списка вершин в оптимальном пути),
ответ1
2
6
13
15
24
32
55
70
63
31
28
47
17
19
29
61
58
57
56
48
37
27
36
38
49
51
50
52
60
59
62
41
64
68
такой же.
Если я не так понял вопрос или линейная сложность - все еще долго, то стоит уточнить размерность графа, и думать в сторону parallel bfs



