Как построить матрицу проективного преобразования без сторонних библиотек?

Question

[andreyk6]

Добрый день.

Хочу решить эту задачу, но не смог найти ответа на то, как построить матрицу проективного преобразования без использования сторонних библиотек (OpenGL, OpenCV, ...).
Прочитал много материала на эту тему, читал статью на Хабре.

Задача следующего вида:
Даны: правильный четырехугольник и квадрат, которые заданы своими координатами A(x1,y1), B(x2,y2), C(x3,y3), D(x4,y4) и M(0,0), N(1,0), P(1,1), K(0,1) соответственно.
Есть точка P(x,y), которая находится в этом четырехугольнике.
Нужно: Построить матрицу проективного преобразования для преобразования ABCD в квадрат MNPK. Далее нужно найти положение точки P`(x`,y`) в квадрате.



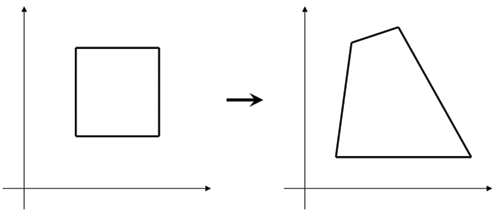
Понял принцип построения такой матрицы. Не могу понять, как реализовать решение системы уравнений в коде.
Буду благодарен, если подскажете правильный путь для решения этой задачи.
Несколько дней убил на поиск решения в интернете, а результата - почти ноль.

Comments

[Mahankov]

Андрей, подскажите, как в итоге строится матрица преобразования? Никак не могу найти верное решение...

Answer 1

[Mrrl]

Проще всего сначала построить матрицу преобразования из квадрата в 4-угольник, а потом взять обратную.
Точки плоскости будем записывать, как принято в компьютерной графике, как строки: (x y 1) для собственной точки и (x y 0) для несобственной. Строка (c* c*y c) обозначает ту же точку, что и (x y 1) (при с!=0).
Пусть матрица преобразования M=((a11 a12 a13) (a21 a22 a23) (a31 a32 a33)). Точка (u,v) квадрата переходит в точку (x,y) четырёхугольника, если для некоторого с!=0 выполняется
(u v 1)*M=(c*x c*y c).
Сначала возьмём вершину (0,0). Получим
a31=c1*x1, a32=c1*y1, a33=c1. Видно, что мы можем взять a33=c1=1 (матрица тоже определена с точностью до пропорциональности), и у нас есть последняя строчка:
a31=x1, a32=y1, a33=1.
Теперь подставим остальные вершины. Получим 9 уравнений:
a11+x1=c2*x2
a12+y1=c2*y2
a13+1=c2
a11+a21+x1=c3*x3
a12+a22+y1=c3*y3
a13+a23+1=c3
a21+x1=c4*x4
a22+y1=c4*y4
a23+1=c4
Это квадратная система из 9 линейных уравнений. Её легко решить методом Гаусса. А можно вручную исключить все переменные, кроме c2,c3,c4, получить систему из 3 уравнений, решить каким-нибудь методом Крамера (через определители) и восстановить a11,a12,...,a23.
Потом уже посчитать матрицу, обратную к построенной. Можно тоже через определители.

Comments

[andreyk6]

Знаете, вы меня выручили.

[andreyk6]

Час назад, по ошибке, нашел решение для преобразования из квадрата в четырехугольник. Теперь я знаю, что осталось совсем чуть-чуть!

[andreyk6]

Я без метода Гаусса посчитал. Это было относительно легко

Answer 2

[Teivaz]

Comments

[andreyk6]

Спасибо, мне это поможет.
Но, я хотел найти формулы, при помощи которых можно получить матрицу 3x3 вида [A,B,C; D,E,F; a,b,c] имея лишь координаты вершин четырехугольника и квадрата.