Как сгенерировать числа в заданном диапазоне и нужным распределением?

Question

[Dorothy]

Здравствуйте, есть задача сгенерировать набор чисел в заданном диапазоне и в котором значения будут распределяться около заданных точек.

Например, нужно сгенерировать числа в диапазоне от -10 до 100 на основании такого графика.
В функцию будут поданы границы диапазона и точки, в которых нужно наибольшее скопление чисел с вероятностью выпдаения.

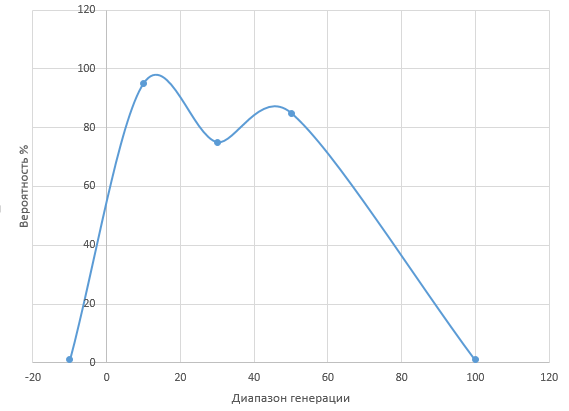
Конкретно для этого графика:
Границы генерации -10, 100. Точки скопления -10 с вероятностью 1%, точка 10 с вероятностью 95%, точка 30 с вероятностью 75%, точка 50 с вероятностью 85%, точка 100 с вероятностью 1%.
И сделать таких точек, например, нужно бы было 15. Результатом могли бы быть числа: 5, 9, 10, 8, 22, 25, 26, 20, 48, 30, 32, 50, 62, 55, 75

Answer 1

[x67]

Наверняка есть готовые библиотеки. Если не найдешь, используй равномерное распределение. Тогда чем шире интервал, тем больше вероятность в него попасть. Приравняй площадь под твоей фигурой к единице, после чего раздели ее на интервалы с необходимой точностью. Площадь каждой фигуры в интервале будет равна вероятности попасть в этот интервал, при том сумма площадей всех таких фигур должна составлять 1. Тогда Можно сгенерировать число с заданным законом. На примере я разделил на три интервала (для тебя их мало будет наверняка, три взял для простоты). Генерим число с помощью равномерного распределения в интервале от 0 до 1, тогда если получилось число в диапазоне (0..0.33), мы попали в первый интервал. Если получилось в диапазоне 0.33..(0.33+0.2), мы попали во второй интервал, ну а 0.53..1 - третий. Сделай таких интервалов 10 и уже красиво будет.
П.с. Сумма вероятностей не может быть больше 100%

Answer 2

[Андрей]

То, что у Вас изображено - плотность вероятности. Вам необходимо из этой функции построить интеграл - функцию вероятности - она всегда идет из значения 0 в начале диапазона, в значение 1 в конце диапазона, но ее форма как раз отражает распределение вероятности в разных частях диапазона (например, для равномерного распределения она будет прямой). Затем Вы генерируете равномерно распределенное число из диапазона [0; 1] и находите искомое Вам с помощью обратной проекции через функцию распределения (сгенерированное число откладываете по Y и смотрите чему равно соответствующее ему на оси X).

Comments

[Dorothy]

Звучит как то, что мне нужно. Я как понимаю, в стандартных библиотеках Python такого нет?

Answer 3

[Sly_tom_cat .]

Тут на лицо распределение по весам.

Нечто подобное я на питоне делал:

wt - входной массив с весами, например [60,30,10] или [60,30,10,5] - сумма не обязательно должна быть равна 100 или какой-то другой величине. Это все учитывается.
Задача выдать индекс в массиве wt с вероятностью пропорциональной весу в этой позиции.

from random import random
wt = [60,30,10]               # массив весов
cw = 0                        # тут будем накапливать веса
rv = random() * sum(wt)       # берем рандом от 0 до 1 и приводим к масштабу (сумма весов)
for j in range(len(wt)):      # проходим по всем весам
  cw += wt[j]                 # прибавляем к аккумулятору вес 
      if cw > rv:             # проверяем не превысил ли накопленный вес случайное значение?
        break                 # если превысил, значит в диапазон этого веса мы и попали.
print(j)                      # печатаем найденный индекс

Answer 4

[Артём Токаревских]

Рисуем прямоугольник от (-10; 100) до (100; 0), включающий заданную кривую.
Методом Монте-Карло бросаем туда точки.
Проверяем координату Y.
Выше заданного графика, игнорируем.
Ниже, считываем координату X.
Повторяем, пока не наберём нужное количество точек.