Генерация всех позможных вариантов заполнения квадратной матрицы N-м числом графов. Алгоритм..?

Question

[Михаил Лубинец]

Здравствуйте.
Возникла необходимость сгенерировать полную выборку возможных вариантов "закраски" матрицы графами.
А точнее их связывания в различных последовательностях. Графы представляют собой ориентированные цепочки.

То есть нужно найти все возможные варианты цепочек элементов, при условии что графов:
а) может быть произвольное количество.
б) "длина" цепочки элементов может варьироваться.
в) матрица произвольного размера, но всегда квадратная.
г) связывать можно только стоящие "рядом элементы" по x или y, никаких диагоналей.

Прошу помощи в поиске оптимального алгоритма, или хотя бы рабочего, для которого можно доказать что полученная выборка будет полной.

UPD: немного переформулирую: нужно найти все варианты связывания элементов в цепочки. (минимум по 2 элемента, дабы сократить количество вариантов)

Для 2х2


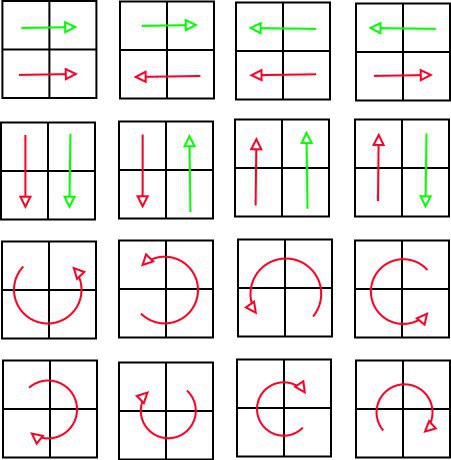
Соответственно для 3х3 и более разница будет в том, что цепочки могут быть сложных форм и разных длинн. И разного количества, в каждом варианте.

Comments

[Андрей]

1. Каков примерно порядок размера матрицы ?
2. Термин "односвязные" шире, чем "цепочки". Все таки, что Вас интересует ... ?

[Михаил Лубинец]

Андрей: цепочки, неверная формулировка, простите.
Порядок от 3 до 10, потому и хочу полную выборку, при большИх порядках это не реально)

[Mrrl]

То есть, нужно найти все варианты обхода шахматной доски N*N ходом ладьи без самопересечений? Например, для 2*2 их 8?

[Михаил Лубинец]

Mrrl: смотрите upd

[Андрей]

Я вижу один путь через вычурную рекурсию, но алгоритм - нетривиальный. Второй путь - через пространство состояний ячеек - писать легко, но слишком большая доля к отбраковыванию из-за петель и ветвлений орграфа - будет значительно медленнее первого..

[Михаил Лубинец]

Андрей: если не трудно, подскажите пожалуйста оба варианта

[Андрей]

Михаил Лубинец: Жду, не предложит ли кто-то более красивого решения дабы потенциально не изобретать велосипед.

[Mrrl]

Если верить программе, то:
Для N=3 есть 225 разбиений на неориентированные цепочки, 1506 на ориентированные
Для N=4 есть 80986 разбиений на неориентированные цепочки, 2168670 на ориентированные
Для N=5 есть 157190078 разбиений на неориентированные цепочки, 23617031908 на ориентированные
Дальше вряд ли есть смысл считать.
Программа простого перебора состояний заходила в тупик (когда на очередную клетку поставить нечего) меньше, чем в 10% случаев.

[Андрей]

Mrrl: Я прочитал Ваш основной ответ - у Вас полный перебор состояний более "изощренный", чем представлял себе я (4 исходящих направления + 1 останов), вероятно, поэтому так невелика доля отбраковки. Интересная идея.

Answer 1

[Mrrl]

Если мы возьмём любую цепочку, проходящую через все точки (например, змейку или спираль), и разрежем её на куски всеми возможными способами, а потом часть кусков ещё и развернём, у нас уже получится примерно 2^(N^2)/3 вариантов. Уже при N=7 перечислить их нереально (при N=6 их всего 10 миллиардов - это не так много). Но поскольку исходных цепочек (проходящих через все точки) много, а кроме того, не все конфигурации можно получить разрезанием одной цепочки, вариантов будет ещё больше.
Алгоритмы - как рекурсия, так и перебор состояний клеток - не очень сложные. В обоих случаях нужно искать разбиение на неориентированные цепочки, а потом всеми способами задавать их направление.
В случае перебора состояний (он проще) делаем так. Замечаем, что у каждой клетки есть 10 возможных состояний - 4 для конца цепочки (направления, куда из этой клетки цепочка идёт), 4 для клетки, где цепочка поворачивает, и 2 для клетки, через которую она проходит прямо. Кроме того, есть ограничения: цепочка не может упираться в стенку, и общее ребро двух соседних клеток либо пересекается цепочкой с каждой стороны, либо нет. Ну, и не должно быть циклов.
Алгоритм получается таким. Перебираете клетки матрицы по строкам. Для каждой очередной клетки смотрите состояние её соседей, и получаете список возможных состояний самой клетки - их не более трёх. В случае, если есть состояние, которое соединяет две соседние цепочки, надо пройтись по ним - проверить, не являются ли они концами одной цепочки (если да - получится цикл, а он запрещён). Теперь подставляем в клетку по очереди все допустимые состояния, и рекурсивно вызываем функцию перебора для следующей клетки. Когда дойдём до конца - фиксируем найденное разбиение.