Как сократить число дуг в орграфе с сохранением «степени» вершин?

Question

[Ernesto Guevara]

Введем понятие "степени" вершины d(x) ориентированного графа как разницу полустепени исхода и полустепени захода. Простыми словами: d(x) = сумма_весов_исходящих_дуг - сумма_весов_входящих_дуг
Получается, что сумма "степеней" всех вершин равна нулю.

Задача: построить на основе заданного графа новый граф с таким же набором вершин с такими же d(x), но с минимальным числом дуг и с минимально возможными весами этих дуг. Можно строить несвязный граф.

Пример:


Дискретную математику изучал сравнительно давно и многое забыл уже. Такая задача всплыла в моем проекте. Сам сходу решить не смог, а что-то подобное не могу найти, но есть ощущение, что это какая-то классическая задача. Прошу прощения, если не использовал устоявшуюся терминологию.

Answer 1

[Ernesto Guevara]

Кажется, я нашел ответ на вопрос. Здесь подобная задача:
stackoverflow.com/questions/15723165/algorithm-to-...

В ответах дана публикация про эту задачу, которая, похоже, NP-полна. Буду изучать.

Answer 2

[mamkaololosha]

1) Строите минимальное остовное дерево, игнорируя веса
en.wikipedia.org/wiki/Minimum_spanning_tree
2) Проставляете веса

Comments

[Ernesto Guevara]

Пункт 2 не совсем понятен. По какому алгоритму проставить веса?

[Ernesto Guevara]

Забыл указать в вопросе, что неважно связный граф получится или нет. Главное, чтобы удовлетворялось мое условие с сохранением разницы весов.

[Mrrl]

Сначала надо разбить на максимальное число связных компонент с нулевой суммой весов в каждой - тогда останется меньше рёбер. А кроме того, если построить произвольное дерево, то веса в нём могут получиться отрицательными. Так что с этим придётся как-то бороться.

Answer 3

[Mrrl]

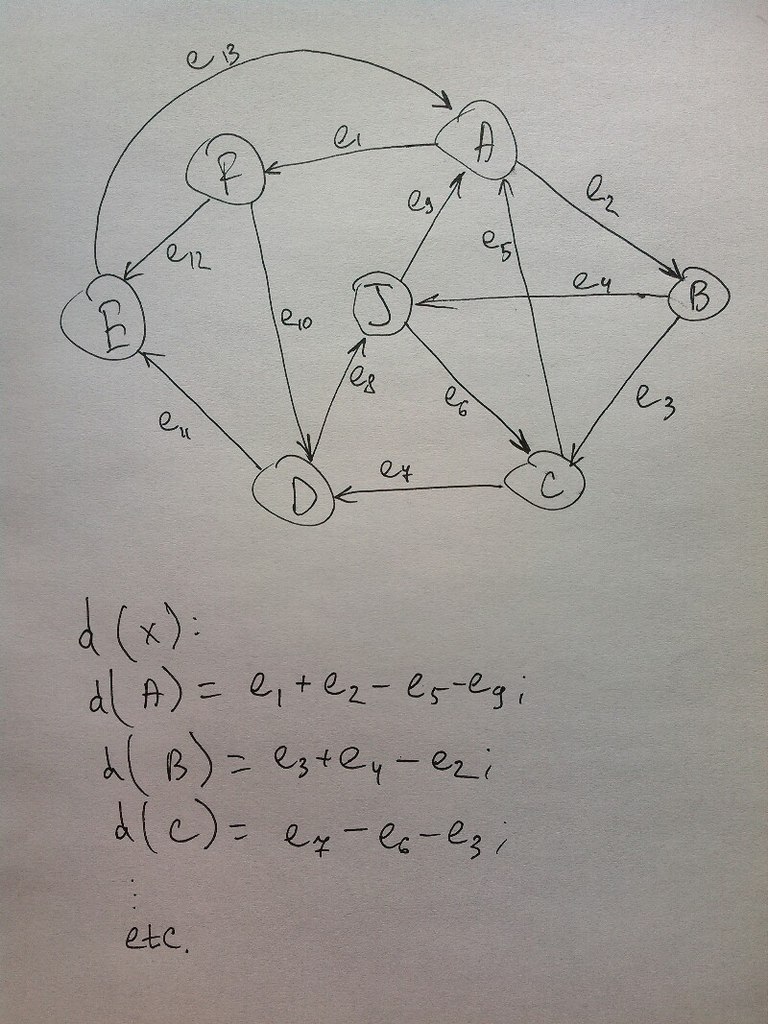
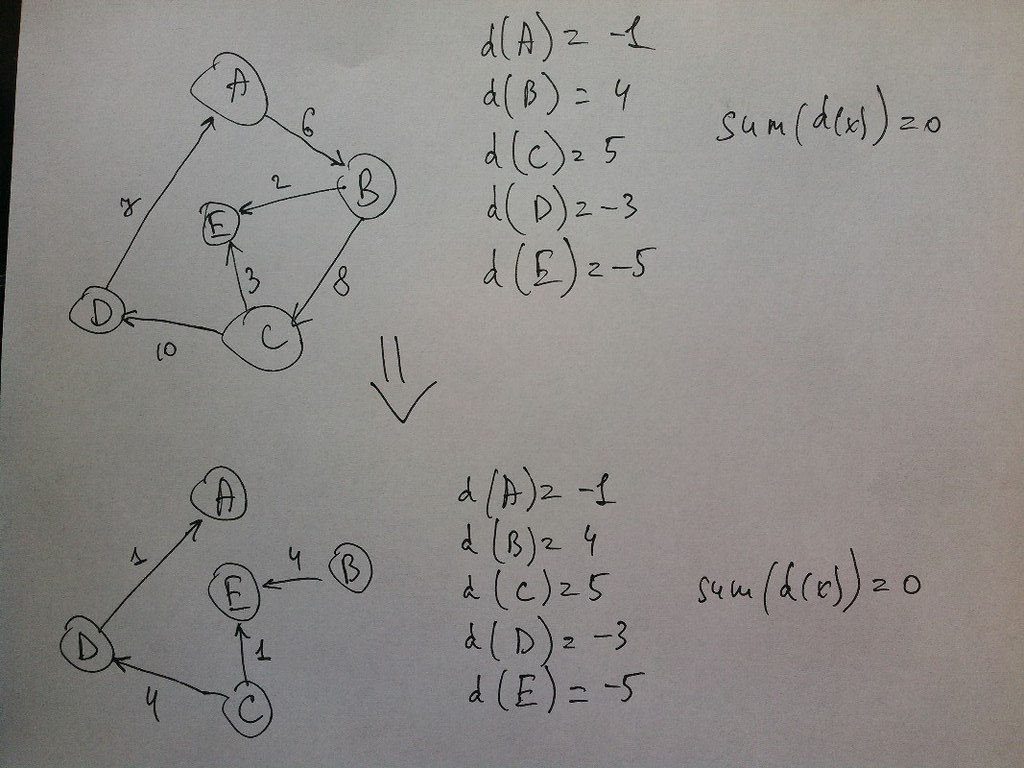Проще всего - найти произвольный цикл, в нём - ребро наименьшего веса, и вычесть этот вес из всех рёбер. Продолжать, пока циклов не останется. Но результат может быть сильно неоптимальным.
Можно искать цикл, в котором наименьший вес ребра максимален (добавлять рёбра начиная с самого тяжёлого, пока в графе не появится цикл). Тогда результат должен получиться заметно лучше (по сумме весов). Но число рёбер может быть не минимальным.
Кстати, можно ли увеличивать веса дуг (из графа (1,2,w=1), (2,3,w=2), (1,3,w=4) получить (2,3,w=1),(1,3,w=5))? Если да, то после того, как циклы в ориентированном графе кончились, придётся искать циклы в неориентированном графе, и прибавлять ко всем рёбрам наименьший по модулю вес ребра с учётом направления рёбер (вычитать из попутных и прибавлять ко встречным).

Comments

[Ernesto Guevara]

Спасибо за ответ. Про циклы я тоже догадался и начал уже искать другие способы "нормализации", но потом почитал статью: www.mathmeth.com/tom/files/settling-debts.pdf

Если интересно, можете тоже посмотреть. Там автор рассматривает все такие случаи "нормализации", а также говорит о двух вариантах: в приоритете минимальное число дуг или же минимальный суммарный вес всех дуг. В первом случае получается NP-полная задача, для которой точное решение найдется полным перебором.

[Mrrl]

guevara: А для минимального суммарного веса получается задача из линейного программирования?