Как реализовать данное вращение?

Question

[ppxy]

Добрый день.
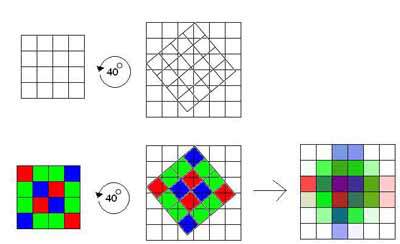
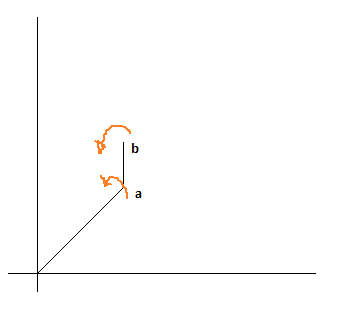
Подскажите, реализация данного движения (см. рисунок):
1) Вращение точки А против часовой стрелки.Начало коортинат (0, 0)
2) Вращение точки B против часовой стрелки. Точка A явсляется началом координат.

Пытался реализовать данное вращение с помощью матриц. Все хорошо только до тех пор, пока точка находится в покое. Делал по формуле T^-1 R T. (смещаемся в 0, вращаемся, возвращаемся). Когда точка A начинает вращение, в данной реализации наблюдается явно не то что должно быть. Хотя я не уверен. Потому что не могу математически обосновать, какое движение будет в результате данных трансформаций.
Вопрос в следующем. Правильно ли я начал делать? (с смещение, вращение, возвращение)
Или же это более сложная задача из области механики?

Есть "реализация на js"

Answer 1

[Сергей Новиков]

Воспользуйтесь oCanvas. Пример с главной страницы очень похож на вашу задачу.

Comments

[ppxy]

Хотелось бы знаеть, как это все реализуется без использования каких либо библиотек и вспомогательных инструментов. Но спасибо.

[Сергей Новиков]

Через боль и страдания, т.е. только с помощью математики. Если вам это нужно чисто для визуализации, то лучше не заморачивать себе голову и воспользоваться библиотекой, в противном случае, да поможет вам Google.

[ppxy]

Нет. Не для визуализации)) Визуализация это второстепенное. Я вроде как разобрался, где был не прав.

Answer 2

[Евгений Петров]

Да вроде несложная — вращение вокруг центра, чьи координаты движутся по круговой орбите.
Если делать матрицами, то вроде как умножать нужно в порядке смещение-вращение.

А если реализовывать подручными средствами, то я предпочту двигать систему координат jsfiddle.net/4e4xtLng/1

Answer 3

[Rsa97]

Пусть R_a и R_b - матрицы поворота точки A относительно O и B относительно A. С - произвольная точка объекта, движение которого задаётся точками A и B. Тогда поворот точки С будет выглядеть так:
С' = R_a×A+R_b×(С-A)
Соответственно, движение точки A:
A' = R_a×A
Движение точки B:
B' = R_a×A+R_b×(B-A)

Answer 4

[ukrainoid]

Можете сравнить с реализацией программного вращения из статьи ukrainoid.com/688x
возможно будет полезнім

Comments

[ppxy]

Интересно. Но вопрос немного не в том.