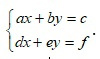Определить, сколько решений имеет система ax + by = c, dx + ey = f?

Question

[Валерий]

Определить, сколько решений имеет система ax + by = c, dx + ey = f
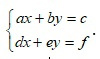
Если решение существует и единственно, то найти значения x и y.
Мой код (сомневаюсь что он правильный):

import numpy
a = int(input("Введите значение переменной Ax: "))
b = int(input("Введите значение переменной By: "))
c = int(input("Введите значение переменной c: "))
d = int(input("Введите значение переменной Dy: "))
e = int(input("Введите значение переменной Ey: "))
f = int(input("Введите значение переменной f: "))
 
if a == 0 and b == 0 and d == 0 and e == 0 and c == 0 and f == 0:
    print("Бесконечное количество решений.")
elif a == 0 and b == 0 and d == 0 and e == 0 and c != 0 and f != 0:
    print("Решений нет.")
else:
    M1 = numpy.array([[a, b], [d, e]])
    v1 = numpy.array([c, f])
    print(numpy.linalg.solve(M1, v1))

Answer 1

[Vindicar]

Представь систему как два графика прямых, и ищи их точку пересечения.

• Если a/d = b/e = с/f, то решений бесконечно много, так как это по сути одно и то же уравнение (одна и та же прямая).
  
• Если a/d = b/e != с/f, то решений нет, так как это уравнения параллельных прямых.
  
• В противном случае есть ровно одно решение, так как у непарарллельных прямых есть одна точка пересечения.
  

Чтобы решить проблему с коэффициентами, равными 0, перестрой пропорцию с деления на умножение.
a/d = b/e = с/f => ae = bd и af = cd
a/d = b/e != с/f => ae = bd и af != cd

Answer 2

[Prizm]

Считаешь детерминанты D = det(((a,b),(d,e))), Dx = det(((c,b),(f,e))) и Dy = det(((a,c),(d,f))) (если пишешь на питоне, то уже должен знать, что это)
x = Dx/D, y=Dy/D.
если D != 0, то решение одно, если D == 0 && (Dx != 0 || Dy != 0), то 0, если D == 0 && Dx == 0 && Dy == 0, то бесконечно.
Аналогично для любой системы n уравнений с n неизвестными