Как вычислить коэффициент уменьшения вписанного в квадрат квадрата под углом n градусов?

Question

[Олег]

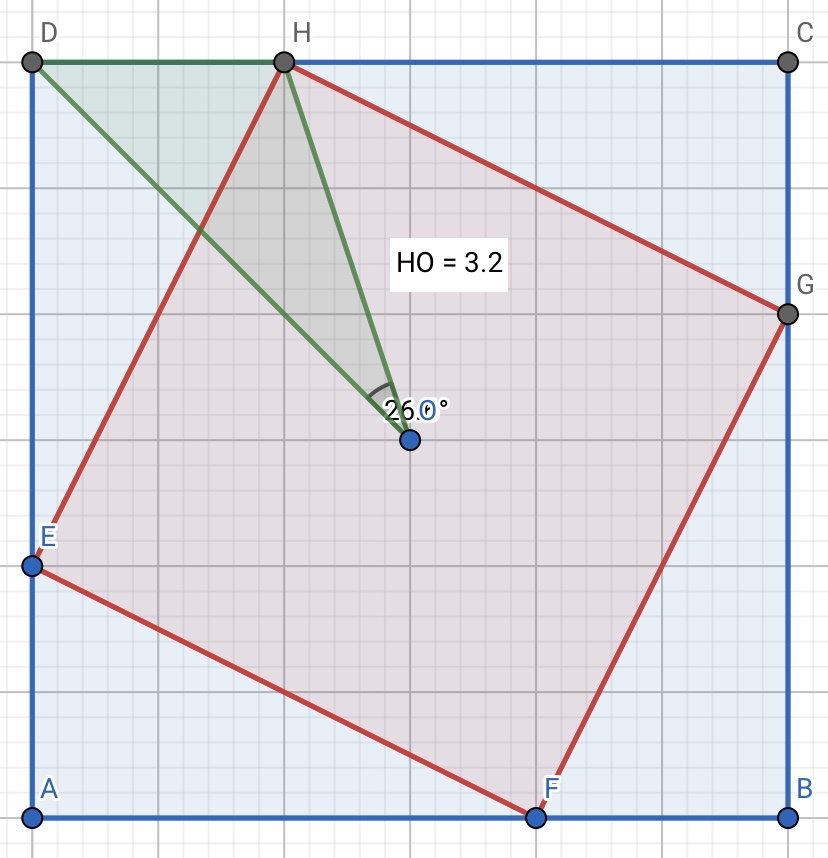
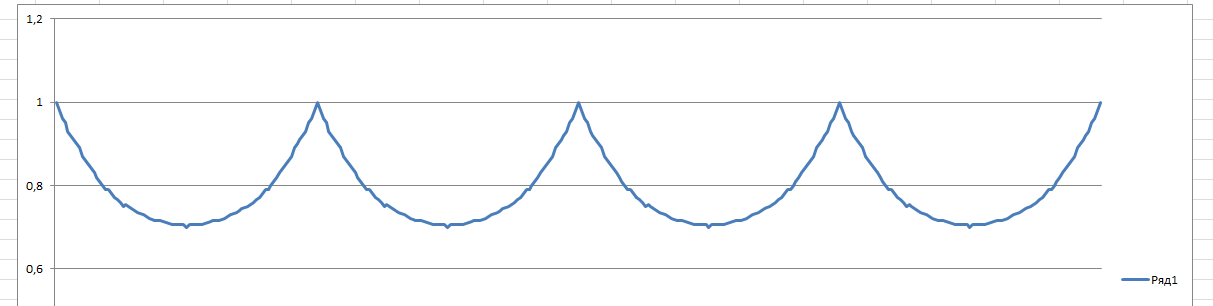
На форме расположен родительский контейнер-квадрат. В нем есть вписанный элемент - тоже квадрат, повернутый на произвольный n-угол при помощи CSS transform:rotate(Ndeg) где N - угол от 0 до 360. При этом нужно, чтобы вписанный квадрат касался родительского контейнера и не выходил за его границы - для этого применяется transform:scale(func(N)) где func(N) - функция, возвращающая коэффициент трансформации для заданного угла. Опытным путем высчитал значения этих коэффициентов для углов 1,2,3...45 , после чего они снова повторяются в обратном порядке и так бесконечно.

Таблицы коэффициентов

const tbl={
0:1,
1:0.98,
2:0.96,
3:0.95,
4:0.93,
5:0.92,
6:0.91,
7:0.9,
8:0.89,
9:0.87,
10:0.86,
11:0.85,
12:0.84,
13:0.83,
14:0.82,
15:0.81,
16:0.8,
17:0.79,
18:0.79,
19:0.78,
20:0.77,
21:0.765,
22:0.76,
23:0.75,
24:0.755,
25:0.75,
26:0.745,
27:0.74,
28:0.735,
29:0.7325,
30:0.73,
31:0.725,
32:0.72,
33:0.7175,
34:0.715,
35:0.7155,
36:0.716,
37:0.713,
38:0.71,
39:0.7075,
40:0.705,
41:0.705,
42:0.705,
43:0.705,
44:0.705,
45:0.7,
46:0.705,
47:0.705,
48:0.705,
49:0.705,
50:0.705,
51:0.7075,
52:0.71,
53:0.7125,
54:0.715,
55:0.7155,
56:0.716,
57:0.718,
58:0.72,
59:0.725,
60:0.73,
61:0.7325,
62:0.735,
63:0.74,
64:0.745,
65:0.7475,
66:0.75,
67:0.755,
68:0.76,
69:0.765,
70:0.77,
71:0.78,
72:0.79,
73:0.79,
74:0.8,
75:0.81,
76:0.82,
77:0.83,
78:0.84,
79:0.85,
80:0.86,
81:0.87,
82:0.89,
83:0.9,
84:0.91,
85:0.92,
86:0.93,
87:0.95,
88:0.96,
89:0.98,
90:1,
}

НО, хранить массив вручную высчитанных коэффициентов (с точностью в 4 знака) как-то думается мне совсем не верный путь. Должна же быть какая-то формула для расчета коэффициента исходя из того что мы знаем угол поворота и все параметры родительского контейнера?

Comments

[Lynn «Кофеман»]

Вспомнить школьную геометрию. Вернее тригонометрию. В частности синус

[Владимир]

Квадрат гипотенузы равен сумме квардратов катетов, осталось найти длинну катетов в зависимости от угла, при этом катет1 = длинна большого квадрата - катет2 + поискать формулу перевода декартовых координат в полярные. Это на вскидку, но не готовое решение.

[iBird Rose]

Задача, конечно, интересная. Но как по мне - хранить данные и вытаскивать в нужное время - именно тут является лучшим решением. Тем более нужно хранить всего 45 значений.

[gracer]

Собственно, интересно в чём задача? Js использовать нельзя?

[Олег]

iBird Rose, Согласен, высчитывать каждый раз это "на-лету" будет слишком расточительно, поэтому я думал заполнить массив коэффициентов при инициализации компонента (один раз) и потом дергать уже этот сформированный массив - просто это избавило бы меня от необходимости видеть в коде 45 строк вручную высчитанных коэффициентов

[Олег]

Lynn «Кофеман», школьная тригонометрия хорошо применяется два раза в жизни - когда сам в школе, и когда уже твои дети туда пошли :)) ... второй этап у меня еще впереди :)

Answer 1

[Григорий Боев]

Внутренняя сторона x
Внешняя kx
В то же время, внешняя это сумма катетов, т.е. xcos(a)+xsin(a).

Тогда k=cos(a)+sin(a)

Answer 2

[Lynn «Кофеман»]

α — угол DOH (насколько повернули квадрат)
β — угол DHO, γ — HDO (45°), DO — половина диагонали исходного квадрата (константа)
β = 180° - α - γ = 135° - α
По теореме синусов при 0° <= α <= 90°
DO / sin(β) = HO / sin(γ) =>
HO = DO * sin(γ) / sin(β) =>
HO = DO / (sqrt(2) * sin(135° - α))


Но как вы хотите запихать эту формулу в CSS это сложный вопрос

Comments

[iBird Rose]

кстати тут же если брать в расчет, что у нас изначально 2 одинаковых квадрата и мы находим на сколько один уменьшить относительно другого - то DO можно всегда брать за единицу же?

[Олег]

... Но как вы хотите запихать эту формулу в CSS это сложный вопрос

- это как раз таки и не проблема. Среда выполнения - Angular-приложение, управление CSS-свойствами реализовано через реактивные функции

[Lynn «Кофеман»]

iBird Rose, да, если нужно отношение, то надо просто поделить на DO
DH/DO = 1/(sqrt(2) * sin(135° - α))
А если таки применить формулу приведения для синуса разности, то получим
DH/DO = 1/(sin α + cos α)
Такой же коэффициент как у Григорий Боев в соседнем ответе.

Его способ, кстати, красивее и мне нравится даже больше моей тригонометрии :)

[Олег]

Lynn «Кофеман», Спасибо большое! получилось то что надо:)

Answer 3

[Олег]

Друзья! Всем большое спасибо за живое участие в решении данной задачи. С геометрической точки зрения вероятно самым простым решением можно считать вариант, предложенный Изобретателем Дикпиков, и если взять контрольный угол в 45 градусов, то коэффициент будет равен 2. НО, в то же время для CSS-scale мне для 45 градусов нужно значение 0,7

Comments

[Lynn «Кофеман»]

Не 0,7, а sqrt(2)/2 ≈ 0,7071