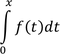Как вычислить интеграл с применением мемоизации на Clojure?

Question

[therealsqvad]

Есть задача:

Реализовать функцию (оператор), принимающую аргументом функцию от одной переменной f и возвращающую функцию одной переменной, вычисляющую (численно) выражение:



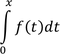
Оптимизировать с использованием мемоизации для задач типа построения графиков (т.е. многократный вызов функции в разных точках) Использовать метод трапеций с постоянным шагом.

(defn trapeze [f x1 x2]
  (*
    (/
      (+ (f x1) (f x2))
      2)
    (Math/abs (- x2 x1))))

(defn integrate [f delta]
  (let [f_memo f
        generate (fn [sum [x1 integral]]
                    (let [x2 (sum x1 delta)]
                      [x2 (+ integral (trapeze f_memo x1 x2))]))
        seq_pos (map first (iterate (partial generate +) [0 0]))
        seq_neg (map first (iterate (partial generate -) [0 0]))]
    (fn [x]
      (let [seq (if (pos? x) seq_pos seq_neg)
            sign (if (neg? x) -1 1)
            x (Math/abs x)
            steps (quot x delta)
            tail (mod x delta)]
        (+
          (nth seq steps)
          (trapeze f_memo
            (* sign (- x tail))
            (* sign x)))
        ))))

Есть проблема с выделенной частью задачи - не могу разобраться с мемоизацией. Кто знает как правильно вынести вычисление частичных сумм и мемоизировать это?

Answer 1

[newpy]

Для мемоизации, существует функция в стандартной библиотеке
(memoize f) которая принимает как аргумент функцию, ссылочно-прозрачную, или иначе говоря чистую функцию.
В вашем контексте это означало бы что что вам необходима чистая функция, многократный вызов которой с одними и теми же аргументами (точками/координатами) должна возвращать один и тот же результат. Ее можно было бы мемоизировать, вышеуказанным способом. Это даст ускорение/быстродействие, при ее многократном вызове, с одними и теми же точками, ценой большего потребления памяти.
Больше наверное не подскажу, это требует большего погружения в детали реализации и математику.