Добрый день!
Имеется следующая задача:
В программе отображается область (по координатам), то есть даны точки границ ее, и можно отрисовать, выглядит примерно так:
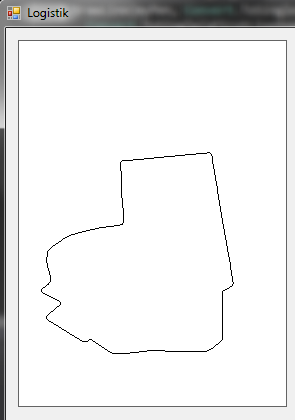
Эту область нужно покрыть прямыми так, например так:
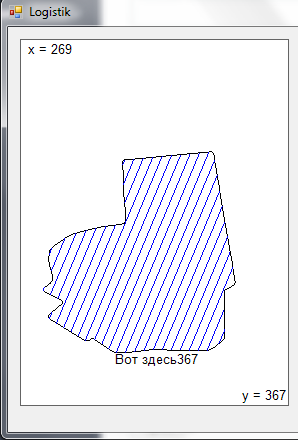
Эти прямые пересекают область в некоторых точках, и за пределами области не рисуются.
Далее нужно повернуть эти прямые, и посчитать сколько раз пересекаются прямые с областью, и так несколько раз, и из всех вариантов выбрать то покрытие, где пересечений минимальное количество.
Не могу реализовать поворот, пишу огромные костыли... :(
ПОМОГИТЕ)
Работаю в Windows Forms, C#. Буду рад любой помощи!


